Các câu hỏi tương tự
Cho hàm số
y
x
−
1
x
+
2
. Phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của đồ thị với trục Ox là A.
y
x
+
3
y
−
1
0
B.
y
x
+
3
y
+
1...
Đọc tiếp
Cho hàm số y = x − 1 x + 2 . Phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của đồ thị với trục Ox là
A. y = x + 3 y − 1 = 0
B. y = x + 3 y + 1 = 0
C. y = x − 3 y + 1 = 0
D. y = x − 3 y − 1 = 0
Cho hàm số y f(x) (ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là A. x – 3y +2 0 B. x + 3y +2 0 C. x – 3y - 2 0 D. x + 3y -2 0
Đọc tiếp
Cho hàm số y = f(x) =(ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y = f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là

A. x – 3y +2 = 0
B. x + 3y +2 = 0
C. x – 3y - 2 = 0
D. x + 3y -2 = 0
Cho a, b, c thỏa mãn
-
1
+
a
-
b
+
c
0
8
+
4
a
+
2
b
+
c...
Đọc tiếp
Cho a, b, c thỏa mãn - 1 + a - b + c > 0 8 + 4 a + 2 b + c < 0 thì số giao điểm của đồ thị hàm số y = x 3 + a x 2 + b x + c với trục Ox là:
A. 1
B. 2
C. 3
D. 0
Tìm số phát biểu đúng trong các phát biểu sau:(1) Đồ thị hàm số y
x
α
với
α
0
nhận trục Ox làm tiệm cận ngang và nhận trục là tiệm cận đứng.(2) Đồ thị hàm số y
x
α
với
α
0
không có tiệm cận.(3) Đồ thị hàm số
y
log
a
x
với
1
a...
Đọc tiếp
Tìm số phát biểu đúng trong các phát biểu sau:
(1) Đồ thị hàm số y= x α với α > 0 nhận trục Ox làm tiệm cận ngang và nhận trục là tiệm cận đứng.
(2) Đồ thị hàm số y= x α với α > 0 không có tiệm cận.
(3) Đồ thị hàm số y = log a x với 1 < a ≠ 1 nhận trục Oy làm tiệm cận đứng và không có tiệm cận ngang.
(4) Đồ thị hàm số y=ax với 1 < a ≠ 1 nhận trục Ox làm tiệm cận ngang và không có tiệm cận đứng.
A. 2.
B. 1
C. 4
D. 3.
cho hàm số \(y=x^2\) và y = -2x+3
a, Vẽ đồ thị của hàm số trên cùng 1 hệ trục tọa độ.
b, Tìm tọa độ giao điểm của 2 đồ thị đó.
Tìm số giao điểm của đồ thị hàm số y = ( x − 2 ) ( x 2 + 3 x + 3 ) với trục hoành.
A. 2
B. 0
C. 1
D. 3
Cho hàm số
y
x
−
1
x
+
2
C
. Phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của (C) với trục Ox là A.
y
1
3
x
−
1
3
B.
y
1...
Đọc tiếp
Cho hàm số y = x − 1 x + 2 C . Phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của (C) với trục Ox là
A. y = 1 3 x − 1 3
B. y = 1 3 x − 1 3
C. y = 1 3 x − 1 3
D. y = 1 3 x − 1 3
Cho hàm số
y
x
−
1
x
+
2
C
.
Phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của
C
với trục Ox là A.
y
1
3
x
−
1
3
B.
y
3
x...
Đọc tiếp
Cho hàm số y = x − 1 x + 2 C . Phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của C với trục Ox là
A. y = 1 3 x − 1 3
B. y = 3 x − 3
C. y = 3 x
D. y = x − 3
Cho hai điểm A, B thuộc đồ thị hàm số y sinx trên đoạn [0;π], các điểm C, D thuộc trục Ox thỏa mãn ABCD là hình chữ nhật và CD 2 π /3. Độ dài của cạnh BC bằng A.
2
2
B.
1
2
C. 1 D.
3
2
Đọc tiếp
Cho hai điểm A, B thuộc đồ thị hàm số y = sinx trên đoạn [0;π], các điểm C, D thuộc trục Ox thỏa mãn ABCD là hình chữ nhật và CD = 2 π /3. Độ dài của cạnh BC bằng
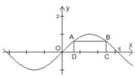
A. 2 2
B. 1 2
C. 1
D. 3 2
Biết rằng đồ thị hàm số bậc 4: y f(x) được cho như hình vẽ sau:Tìm số giao điểm của đồ thị hàm số y g(x) [f’(x)]2 – f(x).f’’(x) và trục Ox A. 0 B. 2 C. 4 D. 6
Đọc tiếp
Biết rằng đồ thị hàm số bậc 4: y = f(x) được cho như hình vẽ sau:
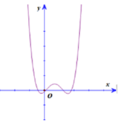
Tìm số giao điểm của đồ thị hàm số y = g(x) = [f’(x)]2 – f(x).f’’(x) và trục Ox
A. 0
B. 2
C. 4
D. 6





