a) Với x ≥ 0 thì √3x có nghĩa. Ta có:
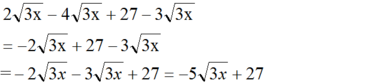
b) Với x ≥ 0 thì √2x có nghĩa. Ta có
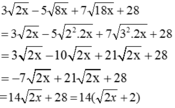
a) Với x ≥ 0 thì √3x có nghĩa. Ta có:
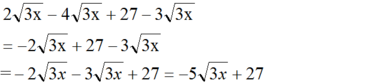
b) Với x ≥ 0 thì √2x có nghĩa. Ta có
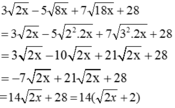
Bài 46. Rút gọn các biểu thức sau với x ≥ 0:
a) 2√3x – 4√3x + 27 – 3√3x
b) 3√2x – 5√8x + 7√18x + 28
rút gọn các biểu thức sau với x ≥ 0
a) \(2\sqrt{3x}-4\sqrt{3x}+27-3\sqrt{3x}\)
b) \(3\sqrt{2x}-5\sqrt{8x}+7\sqrt{18x}+28\)
rút gọn
a)3 √5 + √20-2 √5
b)2 √2+ √8+ √50
c) 4√3+ √ 27 -√45 +2 √5
d) √ 75+ √ 48- √300
e)( √28- √12- √7) √7 +2 √21
f)( √99- √18- √11) √11+3 √22
g)3 √45-5 √125x +7 √20x+28(x>=0)
Cho biểu thức B= (x - 2sqrt(x))/(sqrt(x) - 2) - (2x + 12sqrt(x) + 18)/(sqrt(x) + 3) với x ≥ 0 ,x ≠ 4 Rút gọn B và tìm x để B + 8 > 0 .
Bài 1: Cho biểu thức P = √x √x x-4 √x−2+√x+2) 2√x (với x > 0 và x ≠ 4) a) Rút gọn biểu thức P b) Tìm x để P = 3 Cho biểu thức P = √x √x x-25 + √x-5 √x+5) 2√x (với x > 0 và x ≠ 25) a) Rút gọn biểu thức P b) Tìm x để P = 2
Rút gọn các biểu thức sau với x>= 0:
a)\(2\sqrt{3x}-4\sqrt{3x}+27-3\sqrt{3x}\)
b)\(3\sqrt{2x}-5\sqrt{8x}+7\sqrt{18x}+28\)
Cho hai biểu thức:
A= \(3+\sqrt[3]{-8}.\sqrt{3}+\sqrt[3]{27}.\sqrt{3}-\sqrt{7+4\sqrt{3}}\)
B= \(\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+1}{x-2\sqrt{x}+1}\left(x>0;x\ne1\right)\)
a) Rút gọn A,B
b) Tìm các giá trị của x để B<A?
Help !!!
Rút gọn biểu thức sau với x \(\ge\) 0
a) \(3\sqrt{2x}-4\sqrt{2x}+8-2\sqrt{x}\)
b) \(3\sqrt{2x}-\sqrt{72x}+3\sqrt{18x}+18\)
1. Cho biểu thức: A=\(\left(\frac{x+\sqrt{x}}{\sqrt{x}+1}-\frac{\sqrt{x}-x}{\sqrt{x}-1}\right)\left(1+\frac{1}{\sqrt{x}}\right)\)
a) Rút gọn biểu thức A
b) Tìm giá trị của x để A= 4
2. Rút gọn các biểu thức sau:
a) A= \(3\sqrt{12}-4\sqrt{3}+5\sqrt{27}\)
b) B= \(\frac{1}{\sqrt{7}+4\sqrt{3}}\)
3. Tính giá trị biểu thức D=\(\sqrt[3]{70-\sqrt{4901}}+\sqrt[3]{70+\sqrt{4901}}\)
Cho các biểu thức A = \(\dfrac{\sqrt{x}+3}{\sqrt{x}-2}+\dfrac{\sqrt{x}+2}{3-\sqrt{x}}+\dfrac{2\sqrt{x}-1}{x-5\sqrt{x}-6};B=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\) với x ≥ 0;x ≠ 4;x ≠ 9
a, Tính giá trị của biểu thức B khi x = 25
b, Rút gọn biểu thức A
c, Tìm các giá trị nguyên của x để A > B