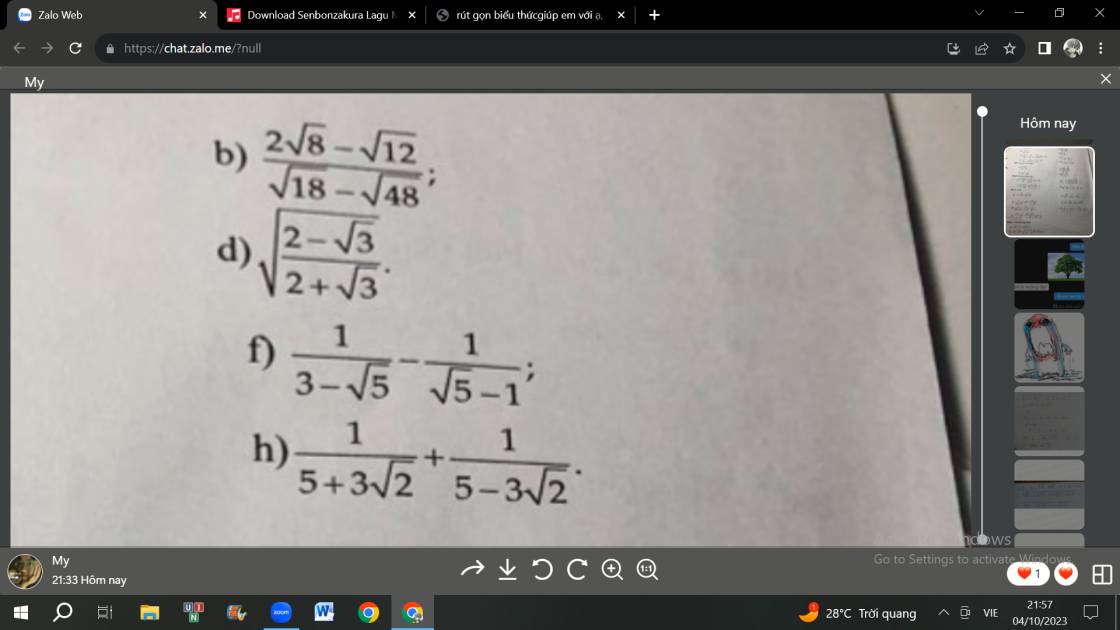
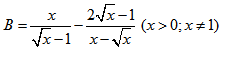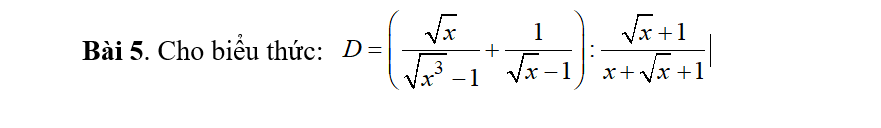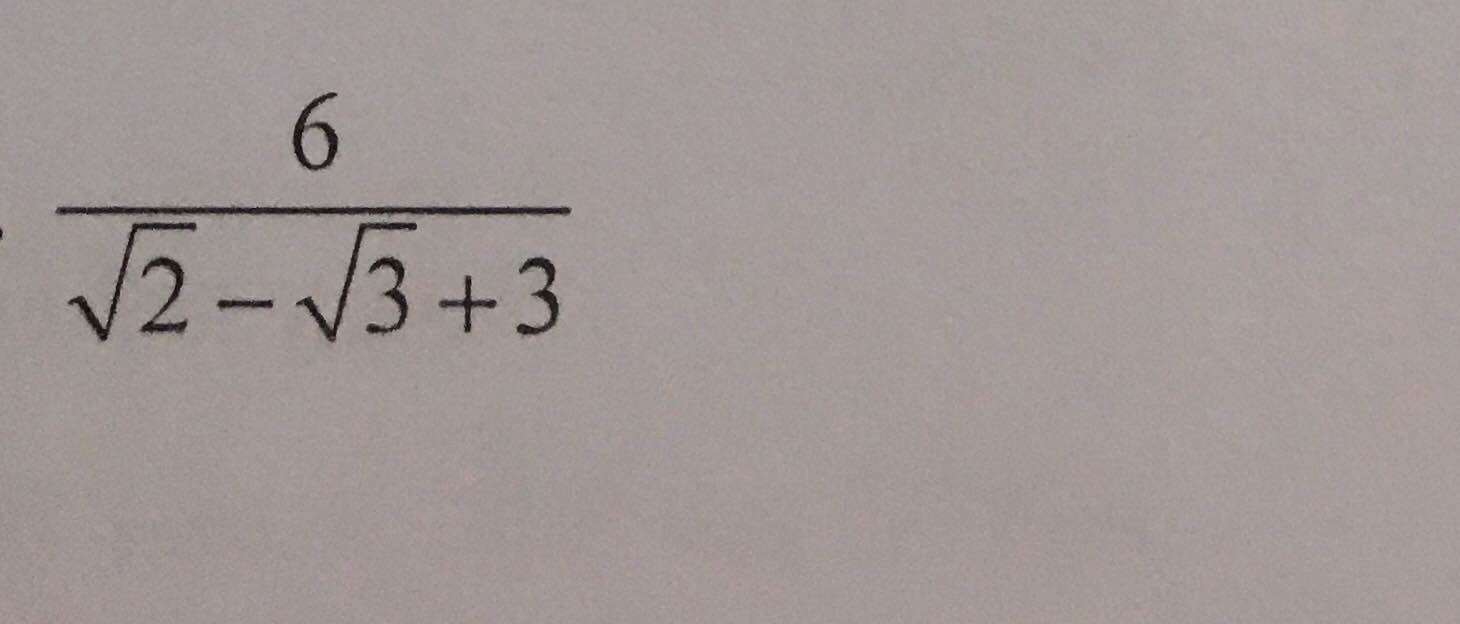b: \(\dfrac{2\sqrt{8}-\sqrt{12}}{\sqrt{18}-\sqrt{48}}\)
\(=\dfrac{2\left(\sqrt{8}-\sqrt{3}\right)}{-\sqrt{6}\left(\sqrt{8}-\sqrt{3}\right)}=-\dfrac{2}{\sqrt{6}}\)
\(=-\dfrac{2\sqrt{6}}{6}=-\dfrac{\sqrt{6}}{3}\)
d: \(\sqrt{\dfrac{2-\sqrt{3}}{2+\sqrt{3}}}\)
\(=\sqrt{\dfrac{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}{\left(2+\sqrt{3}\right)^2}}\)
\(=\sqrt{\dfrac{4-3}{\left(2+\sqrt{3}\right)^2}}=\sqrt{\dfrac{1}{\left(2+\sqrt{3}\right)^2}}\)
\(=\dfrac{1}{2+\sqrt{3}}=2-\sqrt{3}\)
f: \(\dfrac{1}{3-\sqrt{5}}-\dfrac{1}{\sqrt{5}-1}\)
\(=\dfrac{\sqrt{5}-1-\left(3-\sqrt{5}\right)}{\left(3-\sqrt{5}\right)\left(\sqrt{5}-1\right)}\)
\(=\dfrac{\sqrt{5}-1-3+\sqrt{5}}{3\sqrt{5}-3-5+\sqrt{5}}\)
\(=\dfrac{-4+2\sqrt{5}}{-8+4\sqrt{5}}=\dfrac{-4+2\sqrt{5}}{2\left(-4+2\sqrt{5}\right)}=\dfrac{1}{2}\)
h: \(\dfrac{1}{5+3\sqrt{2}}+\dfrac{1}{5-3\sqrt{2}}\)
\(=\dfrac{5-3\sqrt{2}+5+3\sqrt{2}}{\left(5+3\sqrt{2}\right)\left(5-3\sqrt{2}\right)}\)
\(=\dfrac{10}{25-18}=\dfrac{10}{7}\)