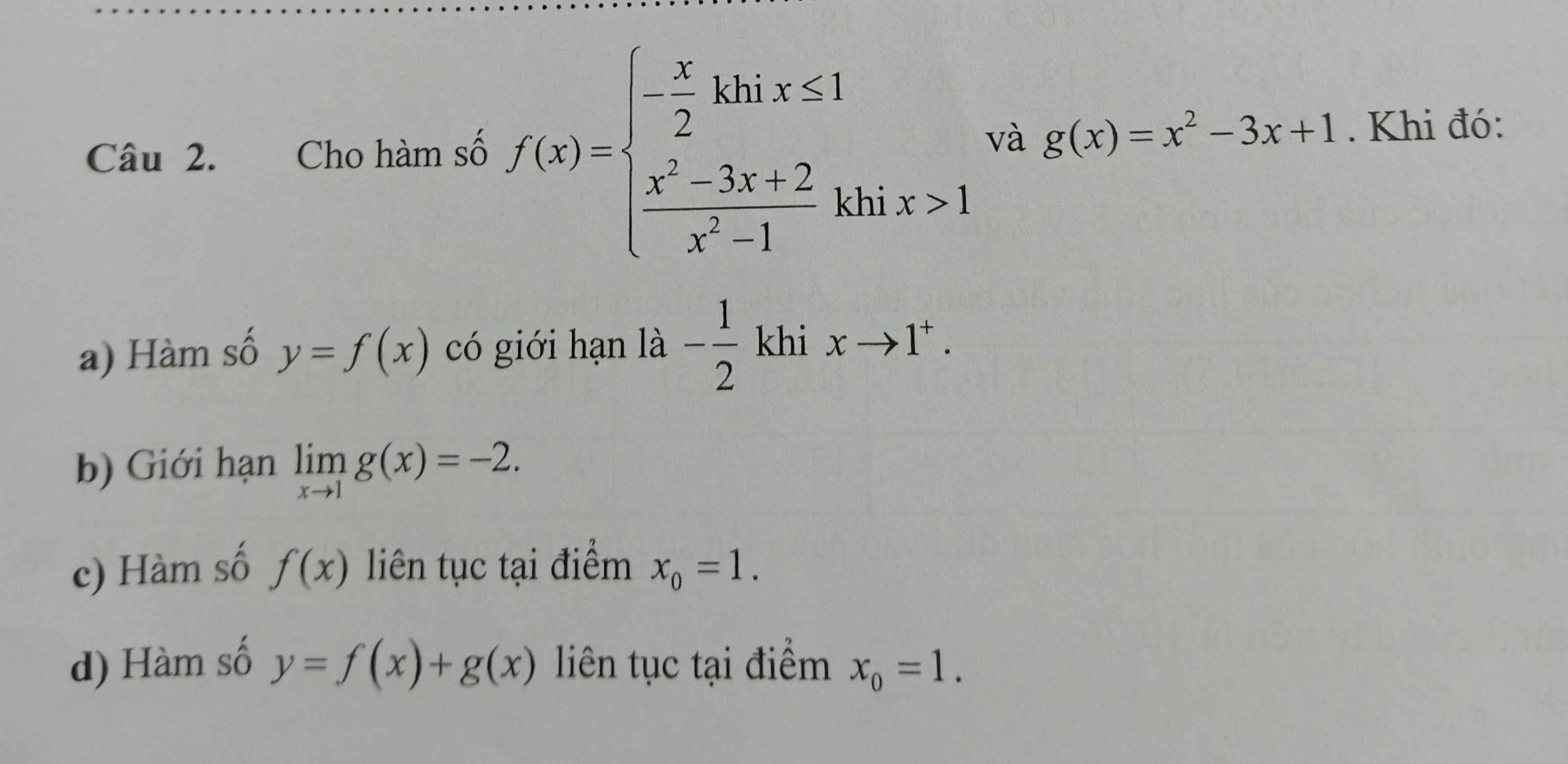a) \(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\dfrac{x^2-3x+2}{x^2-1}=\lim\limits_{x\rightarrow1^+}\dfrac{\left(x-1\right)\left(x-2\right)}{\left(x-1\right)\left(x+1\right)}\)
\(=\lim\limits_{x\rightarrow1^+}\dfrac{x-2}{x+1}=-\dfrac{1}{2}\Rightarrow\) Đúng
b) \(\lim\limits_{x\rightarrow1}g\left(x\right)=\lim\limits_{x\rightarrow1}x^2-3x+1=-1\ne-2\Rightarrow\) Sai
c) \(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}-\dfrac{x}{2}=-\dfrac{1}{2}=\lim\limits_{x\rightarrow1^+}f\left(x\right)\Rightarrow f\left(x\right)\) liên tục tại \(x_o=1\Rightarrow\) Đúng
d) \(\lim\limits_{x\rightarrow1^+}f\left(x\right)+g\left(x\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)+g\left(x\right)=-\dfrac{1}{2}-1=-\dfrac{3}{2}\)
\(\Rightarrow f\left(x\right)+g\left(x\right)\) liên tục tại \(x_o=1\Rightarrow\) Đúng