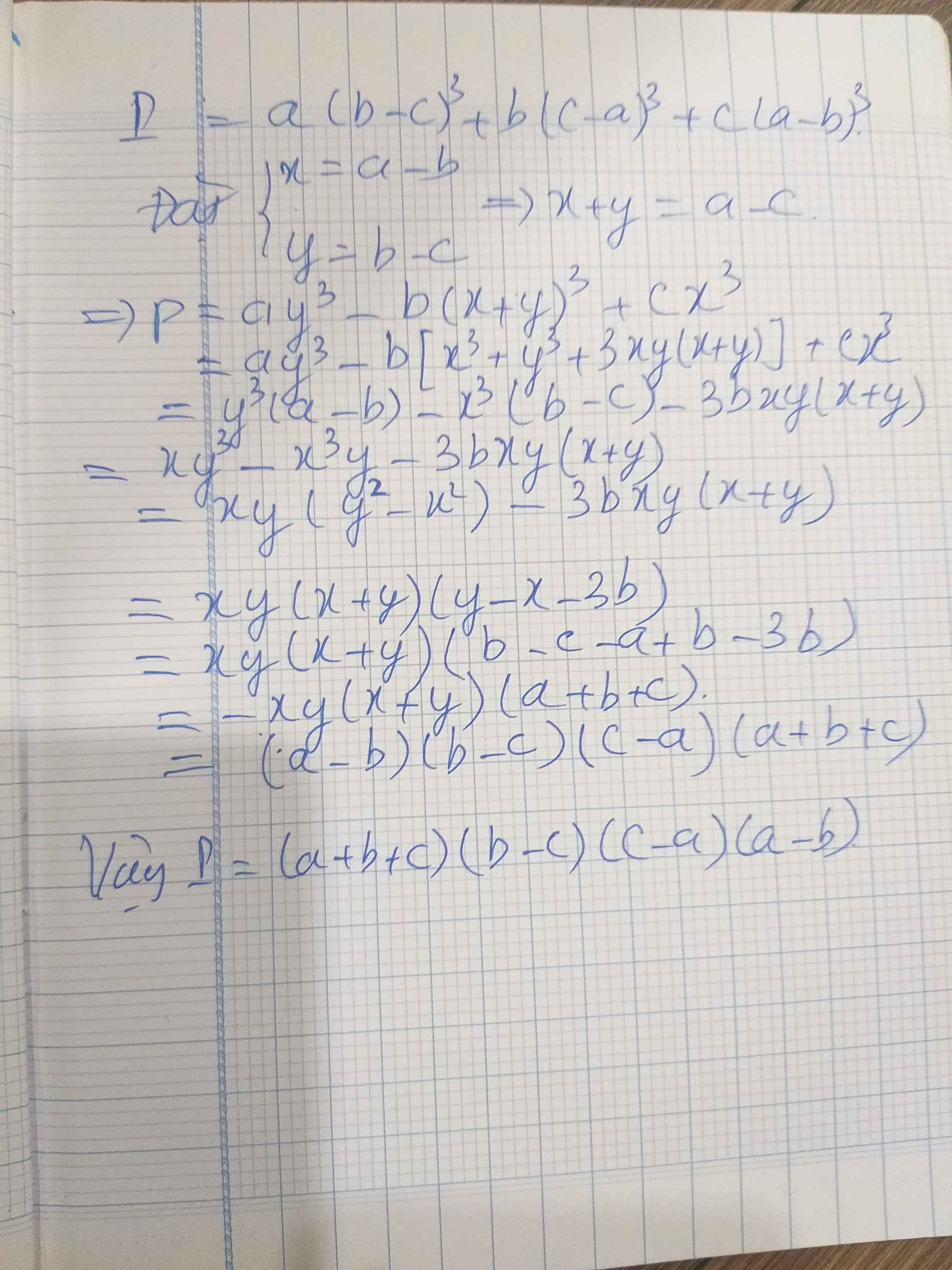Question

Phân tích đa thức thành nhân tử : a(b-c)³+b(c-a)³+c(a-b)³ theo cách xét giá trị riêng hoặc đặt

Answer 1

\(P=a\left(b-c\right)^3+b\left(c-a\right)^3+c\left(a-b\right)^3\)

Đặt \(\left\{{}\begin{matrix}x=b-c\\y=c-a\\z=a-b\end{matrix}\right.\) \(\left(1\right)\)

\(\Rightarrow P=ax^3+by^3+cz^3\)

Ta lại có :

\(x^3+y^3+z^3-3xyz=\left(x+y+z\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)

\(\left(1\right)\Rightarrow x+y+z=0\)

\(\Rightarrow x^3+y^3+z^3=3xyz\)

\(\Rightarrow P=ax^3+by^3+cz^3=3axyz\)

\(\Rightarrow P=a\left(b-c\right)^3+b\left(c-a\right)^3+c\left(a-b\right)^3=3a\left(b-c\right)\left(c-a\right)\left(a-b\right)\)

Answer 2

Sửa lại