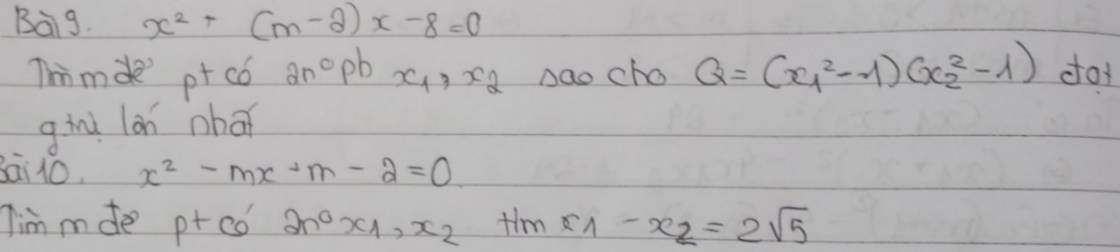9.
\(\Delta=\left(m-2\right)^2+32>0;\forall m\Rightarrow\) pt luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m-2\\x_1x_2=-8\end{matrix}\right.\)
\(Q=\left(x_1^2-1\right)\left(x_2^2-1\right)=\left(x_1x_2\right)^2-\left(x_1^2+x_2^2\right)+1\)
\(=\left(x_1x_2\right)^2-\left(x_1+x_2\right)^2+2x_1x_2+1\)
\(=\left(-8\right)^2-\left(m-2\right)^2+2.\left(-8\right)+1\)
\(=49-\left(m-2\right)^2\)
Do \(\left(m-2\right)^2\ge0;\forall m\)
\(\Rightarrow49-\left(m-2\right)^2\le49\)
Dấu "=" xảy ra khi \(m-2=0\Rightarrow m=2\)
10.
\(\Delta=m^2-4\left(m-2\right)=\left(m-2\right)^2+4>0;\forall m\)
\(\Rightarrow\) Pt luôn có 2 nghiệm với mọi m
Theo hệ thức VietL \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-2\end{matrix}\right.\)
kết hợp điều kiện đề bài và hệ thức Viet ta được:
\(\left\{{}\begin{matrix}x_1+x_2=m\\x_1-x_2=2\sqrt{5}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2x_1=m+2\sqrt{5}\\x_2=x_1-2\sqrt{5}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{m+2\sqrt{5}}{2}\\x_2=\dfrac{m-2\sqrt{5}}{2}\end{matrix}\right.\)
Thế vào \(x_1x_2=m-2\)
\(\Rightarrow\left(\dfrac{m+2\sqrt{5}}{2}\right)\left(\dfrac{m-2\sqrt{5}}{2}\right)=m-2\)
\(\Leftrightarrow m^2-20=4m-8\)
\(\Leftrightarrow m^2-4m-12=0\Rightarrow\left[{}\begin{matrix}m=6\\m=-2\end{matrix}\right.\)