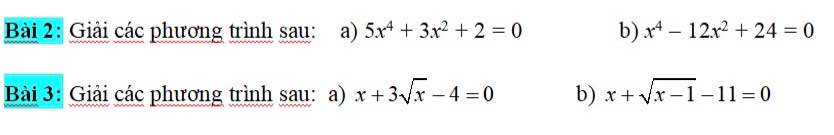a.
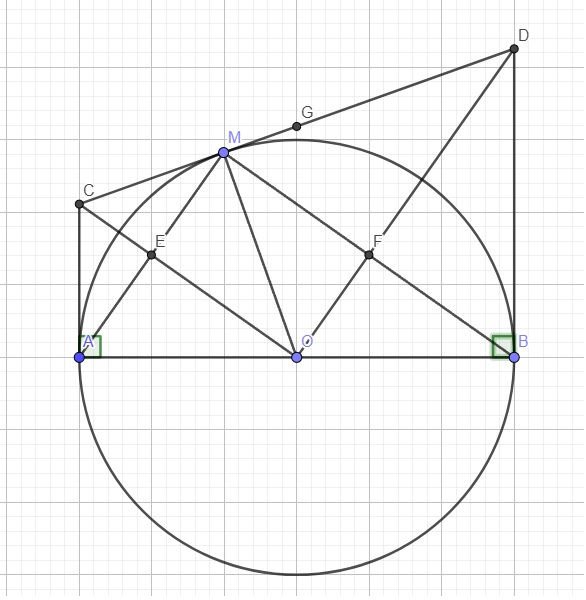
Do C là giao điểm 2 tiếp tuyến tại A và M
\(\Rightarrow AC=MC\)
Tương tự có \(BD=MD\)
\(\Rightarrow AC+BD=MC+MD=CD\)
2.
Cũng theo t/c hai tiếp tuyến cắt nhau ta có:
\(\left\{{}\begin{matrix}\widehat{COA}=\widehat{COM}\\\widehat{DOB}=\widehat{DOM}\end{matrix}\right.\)
\(\Rightarrow\widehat{COA}+\widehat{COM}+\widehat{DOB}+\widehat{DOM}=2\left(\widehat{COM}+\widehat{DOM}\right)\)
\(\Rightarrow180^0=2\widehat{COD}\)
\(\Rightarrow\widehat{COD}=90^0\)
Hay tam giác COD vuông tại O
Trong tam giác vuông COD, do CD là tiếp tuyến tại M \(\Rightarrow OM\perp CD\)
\(\Rightarrow OM\) là đường cao ứng với cạnh huyền
Áp dụng hệ thức lượng:
\(OM^2=CM.MD\Rightarrow R^2=AC.BD\) (do \(AC=CM;BD=MD\))
3.1
Theo cmt ta có \(AC=MC\)
Lại có \(OA=OM=R\)
\(\Rightarrow OC\) là trung trực của AM
\(\Rightarrow OC\perp AM\) tại E
\(\Rightarrow\widehat{OEM}=90^0\)
Hoàn toàn tương tự ta có \(\widehat{OFM}=90^0\)
\(\Rightarrow OEMF\) là hình chữ nhật (tứ giác vó 3 góc vuông)
3.2
\(OM\perp CD\Rightarrow\Delta OCM\) vuông tại M
\(ME\perp OC\Rightarrow ME\) là đường cao trong tam giác vuông OCM
Áp dụng hệ thức lượng:
\(OM^2=OE.OC\Rightarrow OE.OC=R^2\)
Hoàn toàn tương tự ta có: \(OM^2=OF.OD\)
\(\Rightarrow OE.OC=OF.OD=R^2\)
3.3
Do OC là trung trực AM (chứng minh câu 3.1) \(\Rightarrow E\) là trung điểm AM
Tương tự ta có F là trung điểm BM
\(\Rightarrow EF\) là đường trung bình tam giác MAB
\(\Rightarrow EF||AB\)
Mà \(AB\perp BD\) (do BD là tiếp tuyến tại B)
\(\Rightarrow EF\perp BD\)
3.4
Gọi G là trung điểm CD.
Do tam giác COD vuông tại O (theo cm câu 2) \(\Rightarrow\) G là tam đường tròn ngoại tiếp tam giác COD
Hay \(GO\) là 1 bán kính của đường tròn đường kính CD (1)
\(CA\) và BD cùng vuông góc AB \(\Rightarrow CA||BD\Rightarrow ACDB\) là hình thang
O là trung điểm AB, G là trung điểm CD \(\Rightarrow OG\) là đường trung bình hình thang ACDB
\(\Rightarrow GO||DB\Rightarrow GO\perp AB\) tại G (2)
(1);(2)\(\Rightarrow AB\) là tiếp tuyến của đường tròn đường kính CD