Các câu hỏi tương tự
Chứng minh rằng trong tam giác ABC, ta có:
a. tanA + tanB + tanC = tanAtanBtanC 
b. sin2A + sin2B + sin2C = 4sinAsinBsinC
Cho tam giác ABC thỏa mãn:
cos
2
A
+
cos
2
B
sin
2
A
+
sin
2
B
1
2
(...
Đọc tiếp
Cho tam giác ABC thỏa mãn: cos 2 A + cos 2 B sin 2 A + sin 2 B = 1 2 ( c o t 2 A + c o t 2 B ) Tìm mệnh đề đúng?
A. Tam giác ABC là tam giác đều
B. Tam giác ABC là tam giác cân tại C
C. Tam giác ABC là tam giác cân tại A
D. tam giác ABC là tam giác nhọn
Cho A: B; C là các góc nhọn và tanA 1/2, tanB 1/5, tanC 1/8,. Tổng A + B + C bằng
Đọc tiếp
Cho A: B; C là các góc nhọn và tanA = 1/2, tanB = 1/5, tanC = 1/8,. Tổng A + B + C bằng
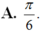
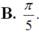
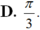
Cho tam giác ABC có \(AB=10\), \(AC=4\)và \(A=60^o\) . Tính chu vi của tam giác ABC, tính tanC
9 tháng 1 2022 lúc 8:41
Cho \(\Delta ABC\), chứng minh rằng:
a) \(\tan A+\tan B+\tan C=\tan A\tan B\tan C\)(\(\widehat{A},\widehat{B},\widehat{C}\)cùng khác \(\frac{\pi}{2}\))
b) \(\sin2A+\sin2B+\sin2C=4\sin A\sin B\sin C\)
9 tháng 9 2023 lúc 15:26
Chứng minh rằng trong tam giác ABC có:
a) tanB = tan( A+C)
b) sinC = sin( A +B)
c) cos A = -cos (B+C)
Nhận dạng tam giác ABC biết :
S=1/4.(p-a).(p-b)
giúp mình với mình cần ngay ạ
Đưa biểu thức A = sin2(a + b) – sin2a - sin2b về dạng tích :
A. A = 2sina.sinb.cos (a + b)
B. A = 2 sina.cosb cos(a + b)
C. A = 2cosa.sinb.cos(a + b)
D. Đáp án khác
Cho biểu thức: A = sin2(a + b) – sin2a - sin2b. Đưa biểu thức trên về dạng tích:
A. A = 2cosa. sinb.sin( a + b)
B. A = 2.sina.cosb.cos(a + b)
C. A = 2cosa.cosb.cos(a + b)
D. A = 2sina.sinb.cos( a + b)