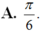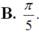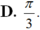Question

Chứng minh rằng trong tam giác ABC, ta có:

a. tanA + tanB + tanC = tanAtanBtanC 

b. sin2A + sin2B + sin2C = 4sinAsinBsinC

Answer 1

Vì A, B, C là ba góc của tam giác nên ta có : A + B + C = π.

⇒ C = π - (A + B); A + B = π - C

a) Ta có: tan A + tan B + tan C = (tan A + tan B) + tan C

= tan (A + B). (1 – tan A.tan B) + tan C

= tan (π – C).(1 – tan A. tan B) + tan C

= -tan C.(1 – tan A. tan B) + tan C

= -tan C + tan A. tan B. tan C + tan C

= tan A. tan B. tan C

b) sin 2A + sin 2B + sin 2C

= 2. sin (A + B). cos (A – B) + 2.sin C. cos C

= 2. sin (π – C). cos (A – B) + 2.sin C. cos (π – (A + B))

= 2.sin C. cos (A – B) - 2.sin C. cos (A + B)

= 2.sin C.[cos (A – B) - cos (A + B)]

= 2.sin C.[-2sinA. sin(- B)]

= 2.sin C. 2.sin A. sin B ( vì sin(- B)= - sinB )

= 4. sin A. sin B. sin C