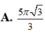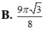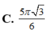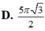Gọi độ dài cạnh tam giác đều là x (m) với \(0\le x\le2\)
\(\Rightarrow\) Độ dài đoạn uốn tam giác đều là \(3x\) (m)
Độ dài đoạn uốn hình vuông là: \(6-3x\) (m)
Diện tích tam giác đều là: \(\dfrac{x^2\sqrt{3}}{4}\left(m^2\right)\)
Độ dài cạnh hình vuông là: \(\dfrac{6-3x}{4}\) (m)
Diện tích hình vuông là: \(\left(\dfrac{6-3x}{4}\right)^2=\dfrac{9x^2-36x+36}{16}\left(m^2\right)\)
Tổng diện tích 2 hình là:
\(f\left(x\right)=\dfrac{x^2\sqrt{3}}{4}+\dfrac{9x^2-36x+36}{16}=\left(\dfrac{9+4\sqrt{3}}{16}\right)x^2-\dfrac{9}{4}x+\dfrac{9}{4}\)
\(f'\left(x\right)=\dfrac{9+4\sqrt{3}}{8}x-\dfrac{9}{4}=0\Rightarrow x=\dfrac{54-24\sqrt{3}}{11}\left(m\right)\)
Vậy độ dài cạnh tam giác đều là \(\dfrac{54-24\sqrt{3}}{11}\left(m\right)\) thì tổng diện tích 2 hình nhỏ nhất
Gọi \(x;y\in Z^+\) lần lượt là số m dây của 2 phần dài 6m
\(\Rightarrow x+y=6\left(1\right)\)
Diện tích tam giác đều : \(\dfrac{x^2\sqrt{3}}{4}\left(m\right)\)
Diện tích hình vuông : \(y^2\left(m^2\right)\)
Tổng diện tích hai hình trên là 1 hàm số : \(z=\dfrac{x^2\sqrt{3}}{4}+y^2\)
\(\Rightarrow z=\dfrac{x^2\sqrt{3}}{4}+\left(6-x\right)^2=\dfrac{x^2\sqrt{3}}{4}+36-12x+x^2\Rightarrow z=\left(\dfrac{4+\sqrt{3}}{4}\right)x^2-12x+36\)
\(\Rightarrow z'=\left(\dfrac{4+\sqrt{3}}{2}\right)x-12\)
\(z'=0\Leftrightarrow\left(\dfrac{4+\sqrt{3}}{2}\right)x-12=0\Leftrightarrow x=\dfrac{24}{4+\sqrt{3}}\)
mà \(\dfrac{4+\sqrt{3}}{4}>0\) nên đồ thị hàm z sẽ đạt cực tiểu tại \(x=\dfrac{24}{4+\sqrt{3}}\) hay tổng diện tích hai hình thu được là nhỏ nhất
Vậy \(\)độ dài cạnh hình tam giác đều là \(\dfrac{24}{4+\sqrt{3}}\left(m\right)\) thỏa mãn yêu cầu đề bài.