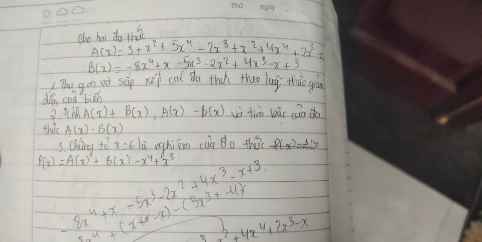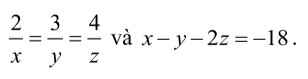Ta có: \(\dfrac{a+b}{c}=\dfrac{b+c}{a}=\dfrac{c+a}{b}\left(a,b,c\ne0\right)\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a+b}{c}=\dfrac{b+c}{a}=\dfrac{c+a}{b}=\dfrac{a+b+b+c+c+a}{c+a+b}=\dfrac{2\left(a+b+c\right)}{a+b+c}=2\)
\(\Rightarrow\left\{{}\begin{matrix}a+c=2b\\b+c=2a\end{matrix}\right.\left(1\right)\)
Thay \(\left(1\right)\) vào \(A\), ta được:
\(A=\dfrac{b}{2b}+\dfrac{2a}{a}=\dfrac{1}{2}+2=\dfrac{5}{2}\)
\(\text{#}Toru\)

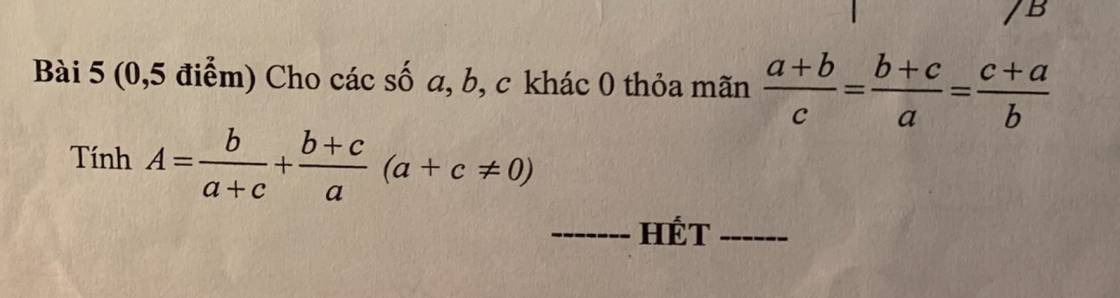








 Mọi người giúp em với ạ
Mọi người giúp em với ạ
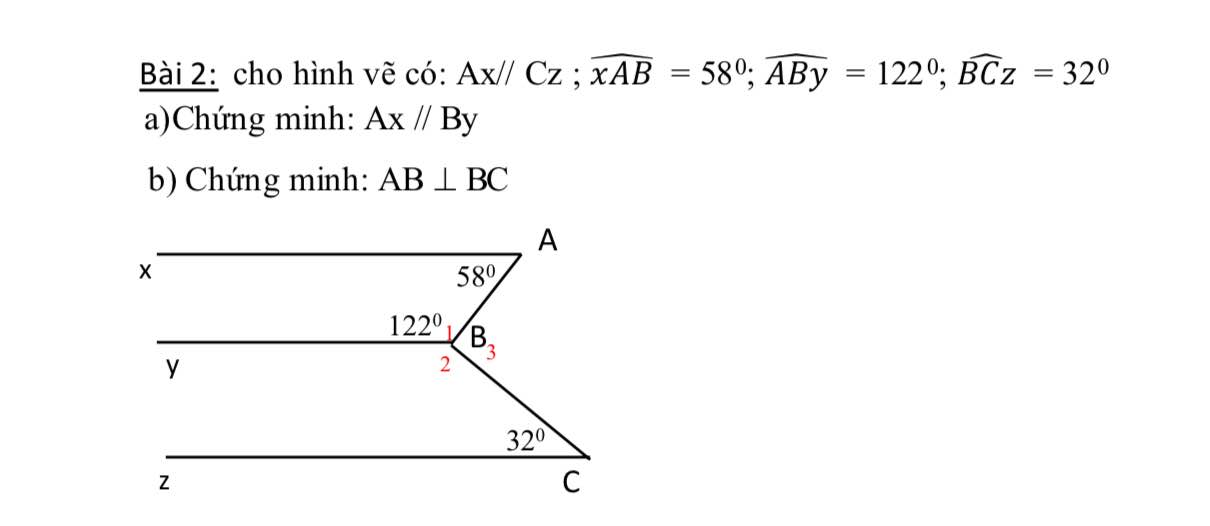
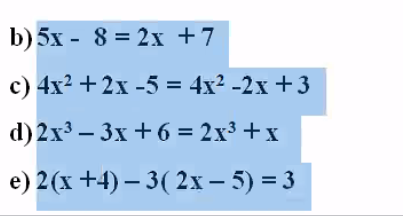 Mọi người ơi ! Giúp em với ạ . Em camon nha !
Mọi người ơi ! Giúp em với ạ . Em camon nha !