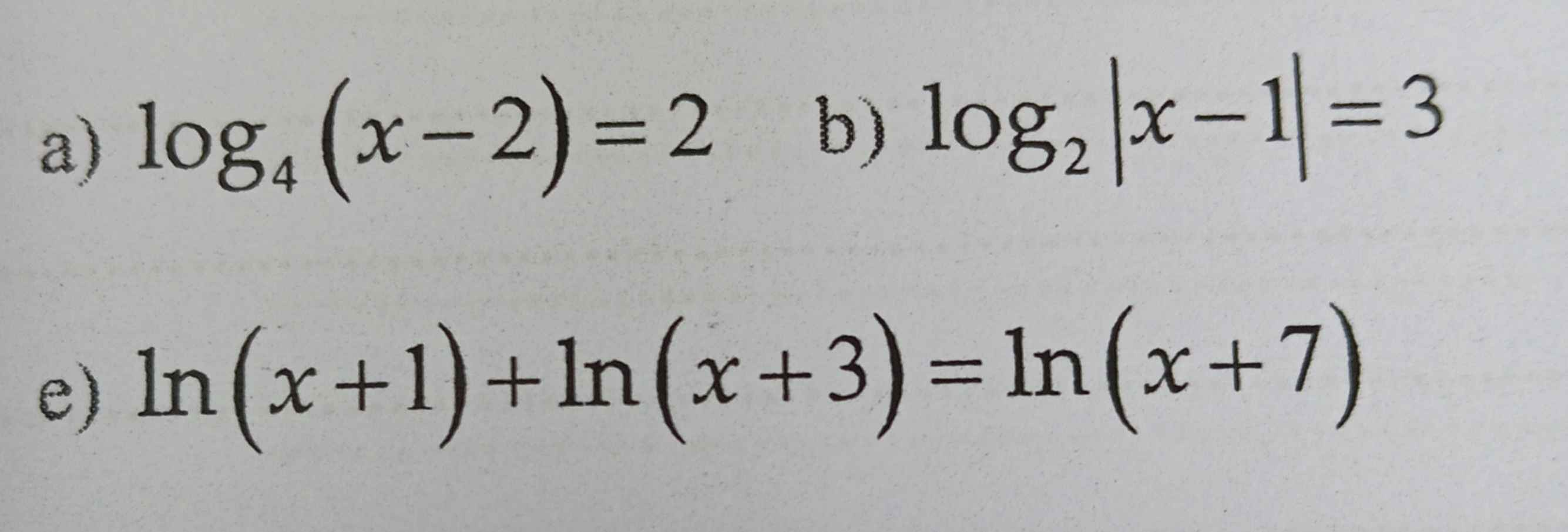a) \(log_{4}(x-2)=2\)
\(x-2 > 0 => x > 2\)
\(4^2 = x-2\) ( định nghĩa logarit)
\(16 = x-2\)
\(x = 18\)
Ta thấy x=18 thoả mãn x>2
----> Nghiệm của phương trình là x = 18
b) \(log_{2}|x-1|=3\)
Ta cần: \( |x-1| > 0\) ( Vì biểu thức trong logarit phải dương)
Điều này đúng với mọi x trừ x = 1.
Chuyển đổi về dạng lũy thừa:
\(2^3 = |x-1| \)
\( 8 = |x-1|\)
\(TH1: x-1 = 8 => x = 9\)
\(TH2: x-1 = -8 => x = -7\)
Cả hai nghiệm (x = 9) và (x = -7) đều thỏa mãn điều kiện \(|x-1| > 0\)
---->Nghiệm của phương trình là x = 9 và x = -7.
\(e) ln(x+1)+ln(x+3)=ln(x+7)\)
Để các logarit tự nhiên có nghĩa:
\(x+1 > 0 => x > -1\)
\(x+3 > 0=> x > -3 \)
\(x+7 > 0 => x > -7\)
Vậy điều kiện xác định chung là \(x > -1\)
\(ln(a) + ln(b) = ln(ab)\)
\(ln(x+1)(x+3) = ln(x+7)\) ( Quy tắc logarit)
Vì hai vế có cùng cơ số (e), ta có thể bỏ logarit và so sánh biểu thức bên trong:
\((x+1)(x+3) = x+7\)
Ta có:
\(x^2 + 4x + 3 = x + 7\)
\(x^2 + 3x - 4 = 0\)
\((x+4)(x-1) = 0\)
Ta có hai nghiệm: x = -4 và x = 1
Trong hai nghiệm, chỉ có x = 1 thỏa mãn điều kiện x > -1
--->Nghiệm của phương trình là \(x = 1\)
a: ĐKXĐ: x>2
\(log_4\left(x-2\right)=2\)
=>\(x-2=4^2=16\)
=>x=18(nhận)
b:
ĐKXĐ: x<>1
\(log_2\left|x-1\right|=3\)
=>\(\left|x-1\right|=2^3=8\)
=>\(\left[{}\begin{matrix}x-1=8\\x-1=-8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=9\left(nhận\right)\\x=-7\left(nhận\right)\end{matrix}\right.\)
e: ĐKXĐ: x>-1
\(ln\left(x+1\right)+ln\left(x+3\right)=ln\left(x+7\right)\)
=>\(ln\left(x^2+4x+3\right)=ln\left(x+7\right)\)
=>\(x^2+4x+3=x+7\)
=>\(x^2+3x-4=0\)
=>(x+4)(x-1)=0
=>\(\left[{}\begin{matrix}x+4=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\left(loại\right)\\x=1\left(nhận\right)\end{matrix}\right.\)