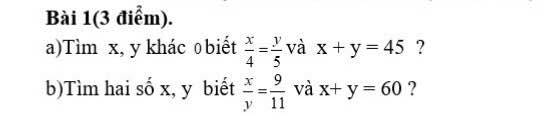a) Ta có: \(\dfrac{x}{4}=\dfrac{y}{5}\) và \(x+y=45\) (1) (\(x,y\ne0\))
Áp dụng tính chất của dãy tỉ số bằng nhau và (1), ta được:
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{x+y}{4+5}=\dfrac{45}{9}=5\)
\(\Rightarrow\left\{{}\begin{matrix}x=5\cdot4=20\\y=5\cdot5=25\end{matrix}\right.\left(tm\right)\)
b) Ta có: \(\dfrac{x}{y}=\dfrac{9}{11}\Leftrightarrow\dfrac{x}{9}=\dfrac{y}{11}\)
Áp dụng tính chất của dãy tỉ số bằng nhau và \(x+y=60\), ta được:
\(\dfrac{x}{9}=\dfrac{y}{11}=\dfrac{x+y}{9+11}=\dfrac{60}{20}=3\)
\(\Rightarrow\left\{{}\begin{matrix}x=3\cdot9=27\\y=3\cdot11=33\end{matrix}\right.\)
Áp dụng t/c dãy tỉ số bằng nhau:
a.
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{x+y}{4+5}=\dfrac{45}{9}=5\)
\(\Rightarrow\left\{{}\begin{matrix}x=4.5=20\\y=5.5=25\end{matrix}\right.\)
b.
\(\dfrac{x}{y}=\dfrac{9}{11}\Rightarrow\dfrac{x}{9}=\dfrac{y}{11}\)
Áp dụng t/c dãy tỉ số bằng nhau:
\(\dfrac{x}{9}=\dfrac{y}{11}=\dfrac{x+y}{9+11}=\dfrac{60}{20}=3\)
\(\Rightarrow\left\{{}\begin{matrix}x=3.9=27\\y=3.11=33\end{matrix}\right.\)