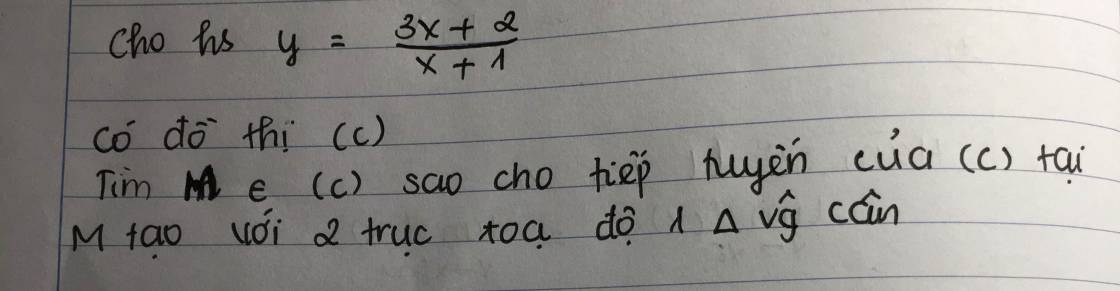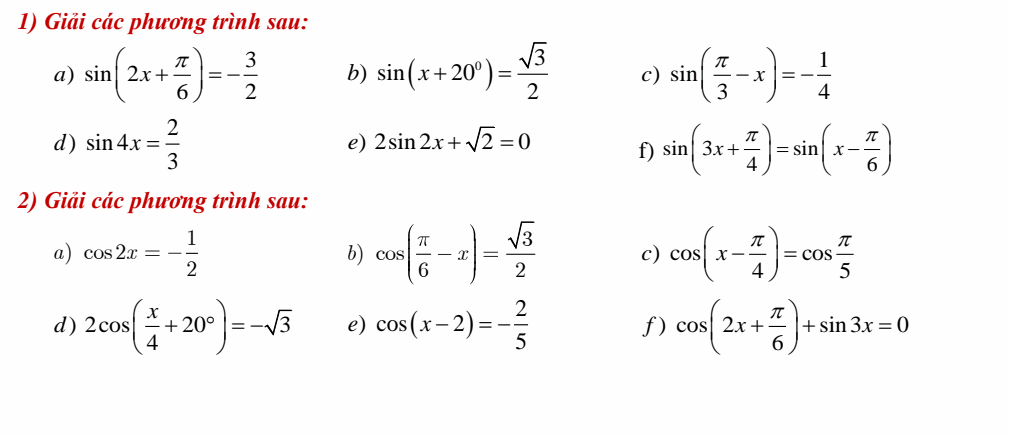a: \(log_{e^2}x>5\)
=>\(\dfrac{1}{2}\cdot log_ex>5\)
=>\(log_ex>5:\dfrac{1}{2}=10\)
=>\(x>e^{10}\)
c:ĐKXĐ: x>-1
\(log_9\left(x+7\right)>log_3\left(x+1\right)\)
=>\(log_3\sqrt{x+7}>log_3\left(x+1\right)\)
=>\(\sqrt{x+7}>x+1\)
=>\(\left\{{}\begin{matrix}x+1>0\\x+7>\left(x+1\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>-1\\x^2+2x+1-x-7< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>-1\\\left(x+3\right)\left(x-2\right)< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>-1\\-3< x< 2\end{matrix}\right.\Leftrightarrow-1< x< 2\)
a. Chuyển đổi cơ số logarit. Ta có thể viết lại bất phương trình như sau
\(\frac{1}{2}log_{e}x > 5\)
vì \(log_{e^2}x\) = \(\frac{log_e x}{log_e e^2}\) =\( \frac{log_e x}{2}\)
Nhân cả hai vế của bất phương trình với 2: \(log_{e}x > 10\)
Viết lại bất phương trình dưới dạng lũy thừa của e: \(x > e^{10}\)
Vậy nghiệm của bất phương trình là \( x > e^{10}\)
c. Chuyển đổi cơ số của logarit thứ nhất về 3:
\(log_{9}(x+7) = \frac{log_{3}(x+7)}{log_{3}9}\) \(= \frac{log_{3}(x+7)}{2}\)
---> \(\frac{1}{2}log_{3}(x+7) > log_{3}(x+1)\)
Nhân cả hai vế của bất phương trình với 2:
\(log_{3}(x+7) > 2log_{3}(x+1) \)
\(log_{3}(x+7) > log_{3}(x+1)^2\)
Vì cơ số logarit là 3 (lớn hơn 1), có thể bỏ logarit và giữ nguyên chiều của bất phương trình:
\(x+7 > (x+1)^2\)
\(x+7 > x^2 + 2x + 1\)
\(0 > x^2 + x - 6\)
\(0 > (x+3)(x-2)\)
Nghiệm của bất phương trình bậc hai này là \(-3 < x < 2\)
Điều kiện xác định của bất phương trình logarit là các biểu thức trong logarit phải dương, tức là:
\(x+7 > 0 => x > -7\)
\(x+1 > 0 => x > -1\)
Kết hợp điều kiện này với nghiệm của bất phương trình bậc hai, ta được nghiệm cuối cùng là: \(-1 < x < 2\)
Vậy nghiệm của bất phương trình là\( -1 < x < 2\)