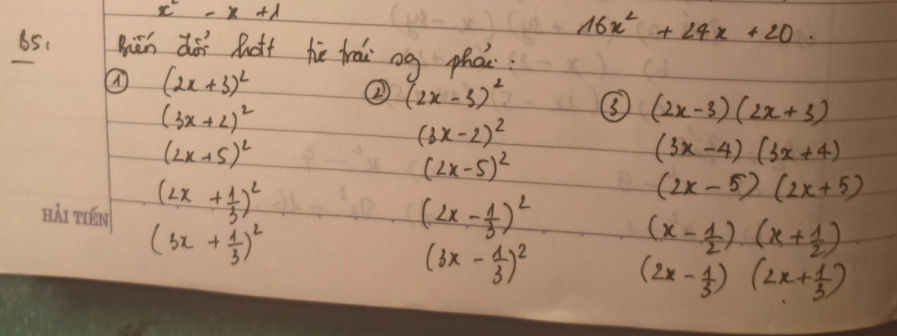1) \(\left(2x+3\right)^2=4x^2+12x+9\)
\(\left(3x+2\right)^2=9x^2+12x+4\)
\(\left(2x+5\right)^2=4x^2+20x+25\)
\(\left(2x+\dfrac{1}{3}\right)^2=4x^2+\dfrac{4}{3}x+\dfrac{1}{9}\)
\(\left(3x+\dfrac{1}{3}\right)^2=9x^2+2x+\dfrac{1}{9}\)
2) \(\left(2x-3\right)^2=4x^2-12x+9\)
\(\left(3x-2\right)^2=9x^2-12x+4\)
\(\left(2x-5\right)^2=4x^2-20x+25\)
\(\left(2x-\dfrac{1}{3}\right)^2=4x^2-\dfrac{4}{3}x+\dfrac{1}{9}\)
\(\left(3x-\dfrac{1}{3}\right)^2=9x^2-2x+\dfrac{1}{9}\)
3) \(\left(2x-3\right)\left(2x+3\right)=4x^2-9\)
\(\left(3x-4\right)\left(3x+4\right)=9x^2-16\)
\(\left(2x-5\right)\left(2x+5\right)=4x^2-25\)
\(\left(x-\dfrac{1}{2}\right)\left(x+\dfrac{1}{2}\right)=x^2-\dfrac{1}{4}\)
\(\left(2x-\dfrac{1}{3}\right)\left(2x+\dfrac{1}{3}\right)=4x^2-\dfrac{1}{9}\)
1: \(\left(2x+3\right)^2=4x^2+12x+9\)
\(\left(3x+2\right)^2=9x^2+12x+4\)
\(\left(2x+5\right)^2=4x^2+20x+25\)
\(\left(2x+\dfrac{1}{3}\right)^2=4x^2+\dfrac{4}{3}x+\dfrac{1}{9}\)
\(\left(3x+\dfrac{1}{3}\right)^2=9x^2+2x+\dfrac{1}{9}\)