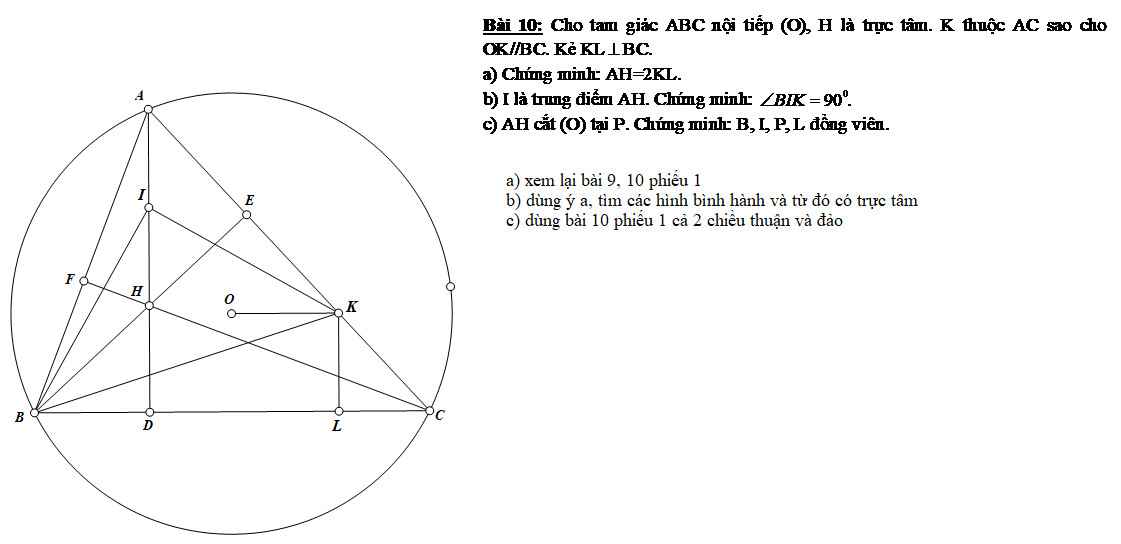
a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(11)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(21)
Từ (11) và (21) suy ra OA là đường trung trực của BC
hay OA⊥BC
b: Xét ΔOBA vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(1\right)\)
Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
Xét ΔBDA vuông tại B có BE là đường cao
nên \(AE\cdot AD=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AE=AH\cdot AO\)
Đúng 0
Bình luận (0)
