Ta có: đường tròn (C1) :
![]()
![]()
Vậy (1) đúng
Đường tròn ( C2):
![]()
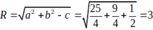
Vậy (2) đúng.
Chọn C.
Ta có: đường tròn (C1) :
![]()
![]()
Vậy (1) đúng
Đường tròn ( C2):
![]()
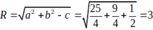
Vậy (2) đúng.
Chọn C.
Cho đường tròn (C): x 2 + y 2 + 4x + 6y + 3 = 0 có tâm I và bán kính R là:
A. I(2;3), R = 10
B. I(2;3), R = 10
C. I(-2;-3), R = 10
D. I(-2;-3), R = 10
Cho đường tròn (C) có phương trình x 2 + y 2 + 4 x − 6 y − 3 = 0 . Khi đó đường tròn có tâm I và bán kính R với
A. I(4; -6), R = 4
B. I(-2; 3), R = 16
C.I(-4; 6), R = 4
D. I(-2; 3) , R = 4
Cho đường tròn (C) có phương trình x 2 + y 2 + 2 x – 8 y + 8 = 0 . Khi đó đường tròn có tâm I và bán kính R với
A. I 2 ; − 8 , R = 2 2
B. I 1 ; − 4 , R = 3
C. I ( - 1 ; 4 ) , R = 3
D. I ( 1 ; - 4 ) , R = 2 √ 2
Đường tròn (C): x 2 + y 2 - 4x - 2y - 20 = 0 có tâm I và bán kính R là:
A. I(-2;-1), R = 25
B. I(2;1), R = 25
C. I(-2;-1), R = 5
D. I(2;1), R = 5
Đường tròn (C): x 2 + y 2 - 4x + 6y - 12 = 0 có tâm I và bán kính R là:
A. I(-2;3), R = 25
B. I(-2;3), R = 5
C. I(2;-3), R = 25
D. I(2;-3), R = 5
Tìm tâm và bán kính của các đường tròn sau:
a, x2 + y2– 2x – 2y - 2 = 0
b, 16x2 + 16y2 + 16x – 8y -11 = 0
c, x2 + y2 - 4x + 6y – 3 = 0
Bài tập :
B1 Viết phương trình đường tròn (C1) có bán kính R1 = 1 , tiếp xúc với trục Ox và có tâm nằm trên đường thẳng denta : 3x - y +7 = 0
B2 Cho đường tròn (C) : x2 + y2 - 2x - 4y - 4 = 0 và đường thẳng (d) : 3x + 4y +4 = 0 . Chứng minh rằng (d) tiếp xúc với (C)
Trong hệ tọa độ Oxy, cho hai đường tròn có phương trình (C1) : x2+ y2- 4y -5 = 0 và (C2) : x2+ y2- 6x + 8y +16= 0 . Phương trình nào sau đây là tiếp tuyến chung của 2 đường tròn.
![]()
![]()
![]()
D. Đáp án khác.
Đường tròn x^2+y^2-4x-6y=12 có tâm I và bán kính R. Với O là gốc tọa độ, mệnh đề nào đúng?
A.OI>R
B. OI=R
C.5OI=R4,123
D.5OI=R3,742