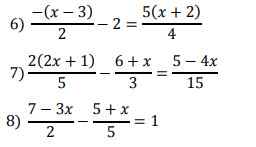Câu 2:
1:
a: a>b
nên -2a<-2b
=>-2a+1<-2b+1
b: a>b
nên 5a>5b
=>5a+1>5b+1>5b-1
2: \(A=x^2+2x+1+4=\left(x+1\right)^2+4>=4\)
Dấu '=' xảy ra khi x=-1
Câu 3:
1) \(\left|x+7\right|=1-2x\) (*)
-ĐK: \(1-2x\ge0\Leftrightarrow-2x\ge-1\Leftrightarrow x\le\dfrac{1}{2}\)
(*) \(\Leftrightarrow x+7=1-2x\) hay \(x+7=2x-1\)
\(\Leftrightarrow x+2x=1-7\) hay \(x-2x=-1-7\)
\(\Leftrightarrow3x=-6\) hay \(-x=-8\)
\(\Leftrightarrow x=-2\) (nhận) hay \(x=8\) (loại)
-Vậy \(S=\left\{-2\right\}\)
2) \(M=a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)=\left(2x+5-x+1\right)\left[\left(2x+5\right)^2-\left(2x+5\right)\left(-x+1\right)+\left(-x+1\right)^2\right]=\left(x+6\right)\left[\left(2x+5\right)^2-\left(2x+5\right)\left(-x+1\right)+\left(-x+1\right)^2\right]>0\)
\(\Rightarrow x+6>0\) và \(\left[\left(2x+5\right)^2-\left(2x+5\right)\left(-x+1\right)+\left(-x+1\right)^2\right]>0\) hoặc \(x+6< 0\) và \(\left[\left(2x+5\right)^2-\left(2x+5\right)\left(-x+1\right)+\left(-x+1\right)^2\right]< 0\)
-Mà \(\left[\left(2x+5\right)^2-\left(2x+5\right)\left(-x+1\right)+\left(-x+1\right)^2\right]\) luôn lớn hơn 0 (bạn tự c/m)
\(\Rightarrow x>-6\)