lm giúp mik vs
Bài 1:
a) \(5x^2y-10xy^2=5xy\left(x-y\right)\)
b) \(4x\left(2y-z\right)+7y\left(z-2y\right)=\left(4x-7y\right)\left(2y-z\right)\)
c) \(5x^2y^3-25x^3y^4+10x^3y^3=5x^2y^3\left(1-5xy+2x\right)\)
d) \(12x^2y-18xy^2-30y^2=6y\left(2x^2-3xy-5y\right)\)
e) \(y\left(a-b\right)-7y^2\left(b-a\right)=\left(y+7y^2\right)\left(a-b\right)\)
f) \(27x^2\left(y-1\right)-9x^3\left(1-y\right)=\left(27x^2+9x^3\right)\left(y-1\right)=9x^2\left(3+x\right)\left(y-1\right)\)
Bài 4:
Ta có: \(n^2\left(n+1\right)+2n\left(n+1\right)\)
\(=\left(n+1\right)\cdot\left(n^2+2n\right)\)
\(=n\left(n+1\right)\left(n+2\right)\)
Vì n;n+1 và n+2 là tích của ba số nguyên liên tiếp nên \(n\left(n+1\right)\left(n+2\right)⋮3!\)
hay \(n\left(n+1\right)\left(n+2\right)⋮6\)
Bài 2:
a: Ta có: \(5\left(x+3\right)-2x\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(5-2x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=\dfrac{5}{2}\end{matrix}\right.\)
b: Ta có: \(4x\left(x-2021\right)-x+2021=0\)
\(\Leftrightarrow\left(x-2021\right)\left(4x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2021\\x=\dfrac{1}{4}\end{matrix}\right.\)
c: Ta có: \(2x^3-32x=0\)
\(\Leftrightarrow2x\left(x^2-16\right)=0\)
\(\Leftrightarrow x\left(x-4\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)
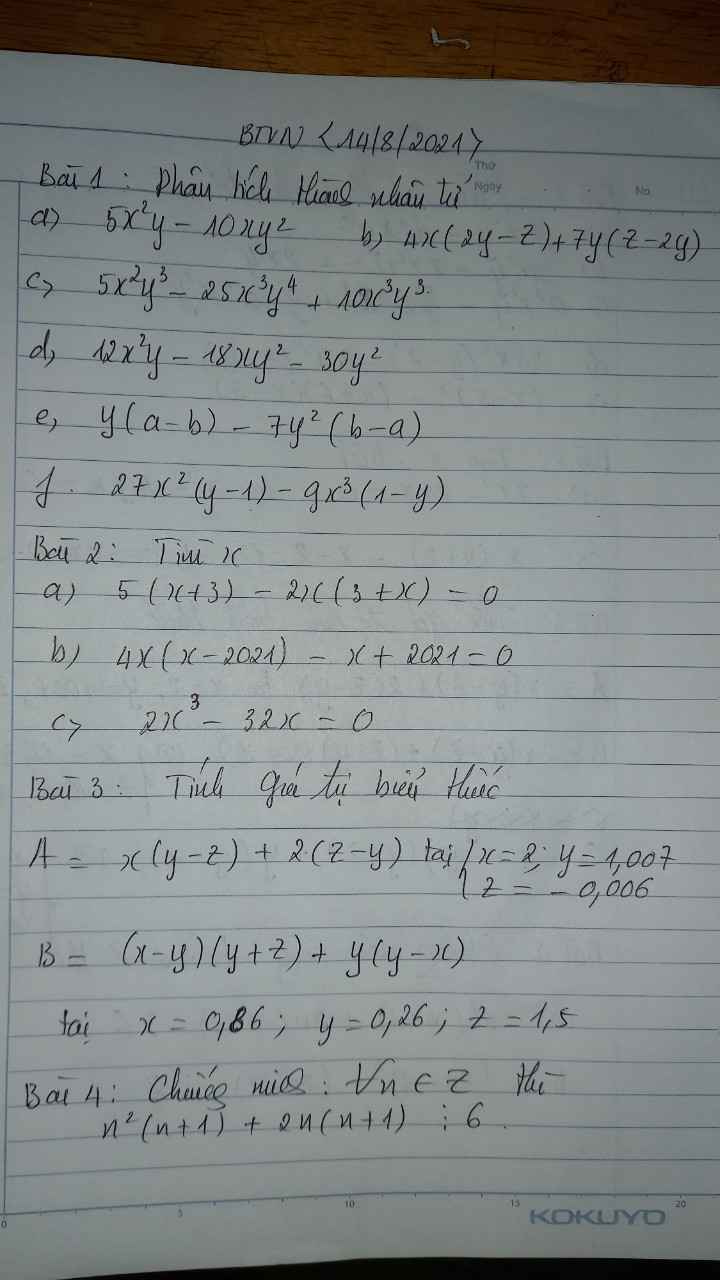lm giúp mik vs mn mik cần gấp
lm giúp mik vs 
lm giúp mik vs 
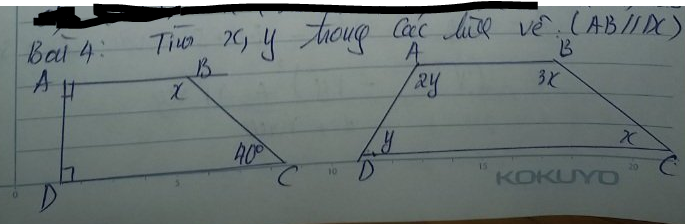lm giúp mik vs chiều nay kt r
