10. Đặt: \(\dfrac{1}{x}=a;\dfrac{1}{y}=b\)
\(=>\left\{{}\begin{matrix}a+b=3\\3a-2b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3-b\\3\left(3-b\right)-2b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3-b\\5b=10\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=3-2=1\\b=2\end{matrix}\right.=>\left\{{}\begin{matrix}\dfrac{1}{x}=1\\\dfrac{1}{y}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\dfrac{1}{2}\end{matrix}\right.\)
11. Đặt: \(\dfrac{1}{y}=k\)
\(=>\left\{{}\begin{matrix}x+k=-\dfrac{1}{2}\\2x-3k=-\dfrac{7}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}-k\\2\left(-\dfrac{1}{2}-k\right)-3k=-\dfrac{7}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}-k\\5k=\dfrac{5}{2}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}-\dfrac{1}{2}=-1\\k=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\\dfrac{1}{y}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\)
15. Đặt: \(\sqrt{x}=a;\sqrt{y}=b\)
\(\left\{{}\begin{matrix}3a+2b=16\\2a-3b=-11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{16-3a}{2}\\2a-3\cdot\dfrac{16-3a}{2}=-11\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{16-3a}{2}\\13a-48=-22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{16-3a}{2}\\13a=26\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{16-3\cdot2}{2}=5\\a=2\end{matrix}\right.\\ =>\left\{{}\begin{matrix}\sqrt{y}=5\\\sqrt{x}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=25\\x=4\end{matrix}\right.\)
14: ĐKXĐ: \(y\ne-2x;y\ne\dfrac{x}{2}\)
\(\left\{{}\begin{matrix}\dfrac{1}{2x+y}+\dfrac{1}{x-2y}=\dfrac{5}{8}\\\dfrac{1}{2x+y}-\dfrac{1}{x-2y}=-\dfrac{3}{8}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{2x+y}+\dfrac{1}{x-2y}+\dfrac{1}{2x+y}-\dfrac{1}{x-2y}=\dfrac{5}{8}-\dfrac{3}{8}\\\dfrac{1}{2x+y}+\dfrac{1}{x-2y}=\dfrac{5}{8}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{2}{2x+y}=\dfrac{2}{8}\\\dfrac{1}{x-2y}=\dfrac{5}{8}-\dfrac{1}{2x+y}=\dfrac{5}{8}-\dfrac{1}{8}=\dfrac{1}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+y=8\\x-2y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2y+2\\2\left(2y+2\right)+y=8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2y+2\\5y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{4}{5}\\x=2\cdot\dfrac{4}{5}+2=\dfrac{8}{5}+2=\dfrac{18}{5}\end{matrix}\right.\left(nhận\right)\)
13: ĐKXĐ: \(\left\{{}\begin{matrix}x\ne-1\\y\ne2\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\dfrac{x+2}{x+1}+\dfrac{2}{y-2}=6\\\dfrac{5}{x+1}-\dfrac{1}{y-2}=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}1+\dfrac{1}{x+1}+\dfrac{2}{y-2}=6\\\dfrac{5}{x+1}-\dfrac{1}{y-2}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x+1}+\dfrac{2}{y-2}=5\\\dfrac{10}{x+1}-\dfrac{2}{y-2}=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{11}{x+1}=11\\\dfrac{1}{x+1}+\dfrac{2}{y-2}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+1=1\\\dfrac{2}{y-2}=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=0\\y-2=\dfrac{2}{4}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\dfrac{5}{2}\end{matrix}\right.\left(nhận\right)\)















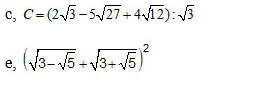
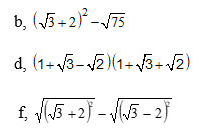 các bạn giải hộ mik mấy câu này vs mik đag cần gấp
các bạn giải hộ mik mấy câu này vs mik đag cần gấp







