Lời giải:
a.
$4x=3y\Rightarrow 20x=15y$
$5y=3z\Rightarrow 15y=9z$
$\Rightarrow 20x=15y=9z=t$
$\Rightarrow x=\frac{t}{20}; y=\frac{t}{15}; z=\frac{t}{9}$
Khi đó:
$2x-3y+z=\frac{2t}{20}-\frac{3t}{15}+\frac{t}{9}=5$
$\frac{t}{90}=6$
$t=540$
$x=\frac{540}{20}=27; y=\frac{540}{15}=36;z=\frac{540}{9}=60$
b. Đặt $5x=8y=3z=t$
$\Rightarrow x=\frac{t}{5}; y=\frac{t}{8}; z=\frac{t}{3}$
Khi đó:
$x-2y+z=34$
$\frac{t}{5}-\frac{2t}{8}+\frac{t}{3}=34$
$\frac{17}{60}t=34$
$t=120$
$x=\frac{120}{5}=24; y=\frac{120}{8}=15; z=\frac{120}{3}=40$
c.
Đặt $\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=t$
$\Rightarrow x=2t; y=3t; z=4t$
Khi đó:
$x^2+3y^2-2z^2=-16$
$(2t)^2+3(3t)^2-2(4t)^2=-16$
$-t^2=-16$
$t^2=16$
$t=\pm 4$
Khi $t=4$ thì $x=2.4=8; y=3.4=12; z=4.4=16$
Khi $t=-4$ thì $x=-8; y=-12; z=-16$
b: Ta có: \(5x=8y=3z\)
\(\Leftrightarrow\dfrac{x}{\dfrac{1}{5}}=\dfrac{y}{\dfrac{1}{8}}=\dfrac{z}{\dfrac{1}{3}}\)
hay \(\dfrac{x}{\dfrac{1}{5}}=\dfrac{2y}{\dfrac{1}{4}}=\dfrac{z}{\dfrac{1}{3}}\)
mà x-2y+z=34
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{1}{5}}=\dfrac{2y}{\dfrac{1}{4}}=\dfrac{z}{\dfrac{1}{3}}=\dfrac{x-2y+z}{\dfrac{1}{5}-\dfrac{1}{4}+\dfrac{1}{3}}=\dfrac{34}{\dfrac{17}{60}}=120\)
Do đó: x=24; y=15; z=40
a: Ta có: 4x=3y
nên \(\dfrac{x}{3}=\dfrac{y}{4}\)
hay \(\dfrac{x}{9}=\dfrac{y}{12}\left(1\right)\)
Ta có: 5y=3z
nên \(\dfrac{y}{3}=\dfrac{z}{5}\)
hay \(\dfrac{y}{12}=\dfrac{z}{20}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{x}{9}=\dfrac{y}{12}=\dfrac{z}{20}\)
hay \(\dfrac{2x}{18}=\dfrac{3y}{36}=\dfrac{z}{20}\)
mà 2x-3y+z=6
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{18}=\dfrac{3y}{36}=\dfrac{z}{20}=\dfrac{2x-3y+z}{18-36+20}=\dfrac{6}{2}=3\)
Do đó: x=27; y=36; z=60

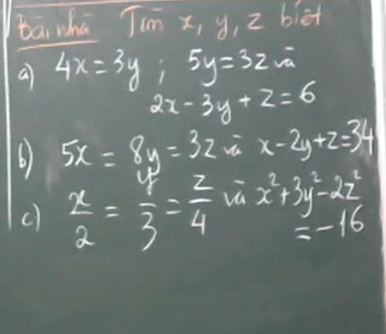




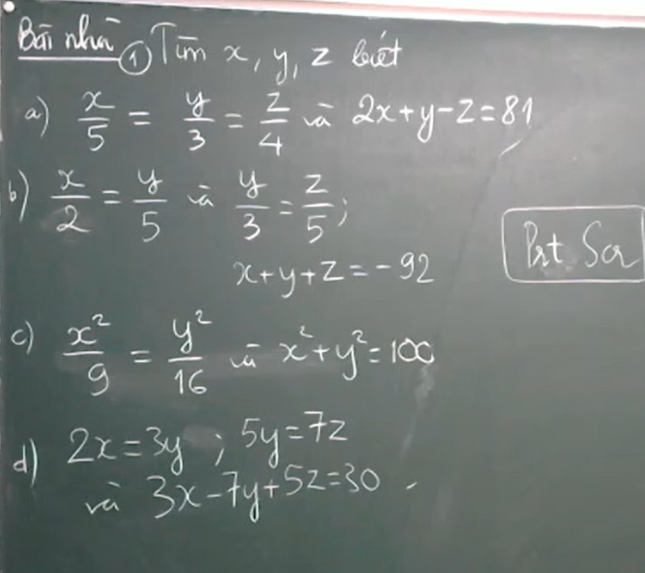






 làm hộ em lần nữa ạ, xin cảm ơn:>
làm hộ em lần nữa ạ, xin cảm ơn:>
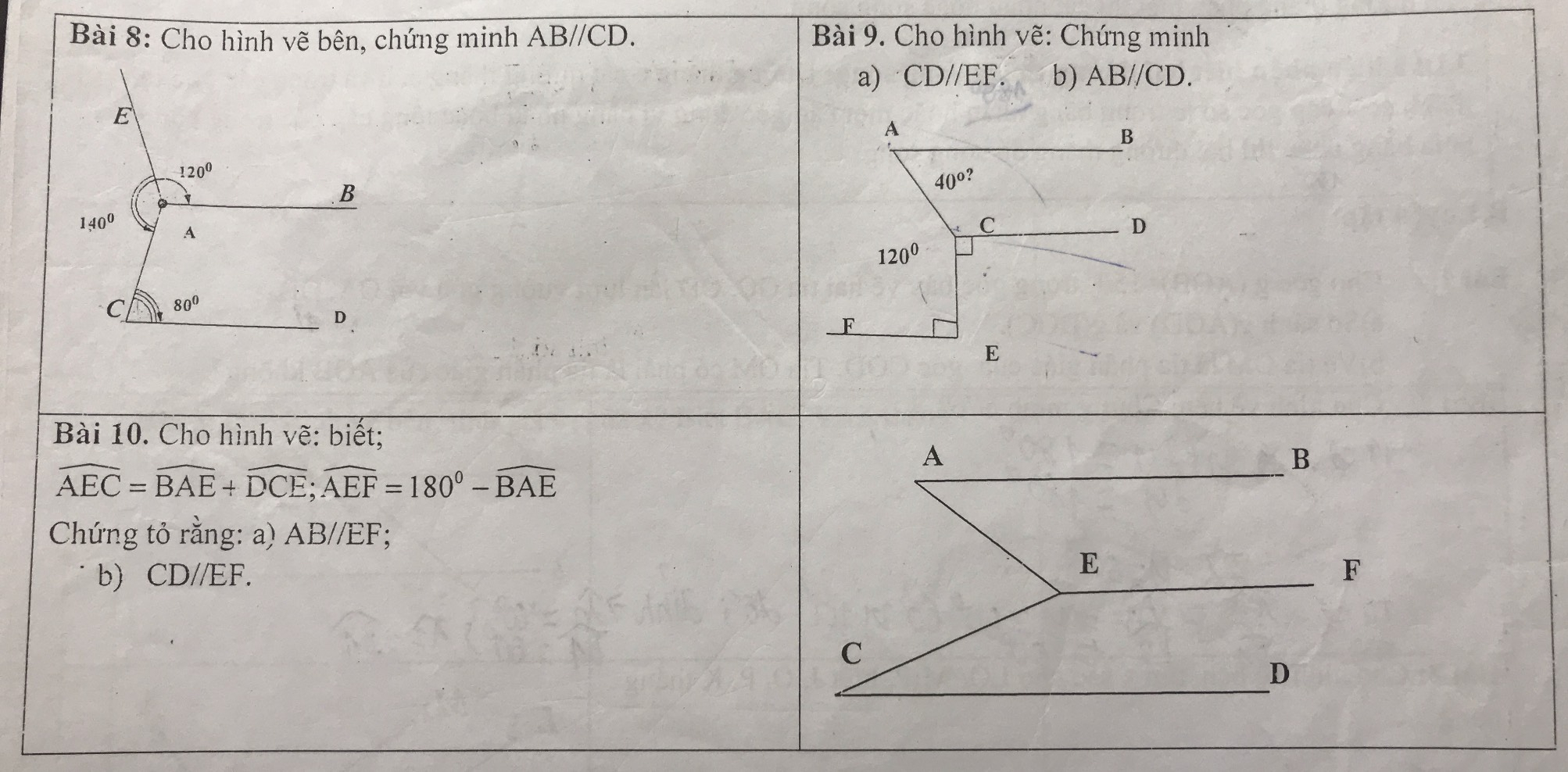 em bài 8,9,10 với ạ em gấp lắm rùi
em bài 8,9,10 với ạ em gấp lắm rùi 

