a) Ta có:
\(\dfrac{x}{5}=\dfrac{2x}{10}=\dfrac{y}{3}=\dfrac{z}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{10}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{2x+y-z}{10+3-4}=\dfrac{81}{9}=9\\ \Rightarrow\left\{{}\begin{matrix}x=9\cdot5=45\\y=9\cdot3=27\\z=9\cdot4=36\end{matrix}\right.\)
Vậy x = 45; y = 27; z = 36.
b) Ta có:
\(\dfrac{x}{2}=\dfrac{y}{5}\)\(\Rightarrow\dfrac{x}{6}=\dfrac{y}{15}\)
\(\dfrac{y}{3}=\dfrac{z}{5}\)\(\Rightarrow\dfrac{y}{15}=\dfrac{z}{25}\)
suy ra, \(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{25}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{25}=\dfrac{x+y+z}{6+15+25}=-\dfrac{92}{46}=-2\\
\Rightarrow\left\{{}\begin{matrix}x=-2\cdot6=-12\\y=-2\cdot15=-30\\z=-2\cdot25=-50\end{matrix}\right.\)
Vậy x = -12; y = -30; z = -50.
c) Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{9+16}=4\\ \Rightarrow\left\{{}\begin{matrix}x^2=36\\y^2=64\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=6\\y=8\end{matrix}\right.\\\left\{{}\begin{matrix}x=-6\\y=8\end{matrix}\right.\\\left\{{}\begin{matrix}x=6\\y=-8\end{matrix}\right.\\\left\{{}\begin{matrix}x=-6\\y=-8\end{matrix}\right.\end{matrix}\right.\)
Vậy (x; y) \(\in\left\{\left(6;8\right);\left(-6;8\right);\left(6;-8\right);\left(-6;-8\right)\right\}\)
d), Ta có:
\(2x=3y\Rightarrow\dfrac{x}{3}=\dfrac{y}{2}\Rightarrow\dfrac{x}{21}=\dfrac{y}{14}\\ 5y=7z\Rightarrow\dfrac{y}{7}=\dfrac{z}{5}\Rightarrow\dfrac{y}{14}=\dfrac{z}{10}\\ \Rightarrow\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}\\ \Rightarrow\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}=\dfrac{3x-7y+5z}{63-98+50}=\dfrac{30}{15}=2\\
\Rightarrow\left\{{}\begin{matrix}x=2\cdot21=42\\y=2\cdot14=28\\z=2\cdot10=20\end{matrix}\right.\)
Vậy x = 42; y = 28; z = 20.
a: Ta có: \(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{4}\)
nên \(\dfrac{2x}{10}=\dfrac{y}{3}=\dfrac{z}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{10}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{2x+y-z}{10+3-4}=\dfrac{81}{9}=9\)
Do đó: x=45; y=27; z=36
b: Ta có: \(\dfrac{x}{2}=\dfrac{y}{5}\)
nên \(\dfrac{x}{6}=\dfrac{y}{15}\left(1\right)\)
Ta có: \(\dfrac{y}{3}=\dfrac{z}{5}\)
nên \(\dfrac{y}{15}=\dfrac{z}{25}\left(2\right)\)
Từ (1), (2) suy ra \(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{25}\)
mà x+y+z=-92
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{25}=\dfrac{x+y+z}{6+15+25}=-\dfrac{92}{46}=-2\)
Do đó: x=-12; y=-30; z=-50
c: Ta có: \(\dfrac{x^2}{9}=\dfrac{y^2}{16}\)
mà \(x^2+y^2=100\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{9+16}=\dfrac{100}{25}=4\)
Do đó: \(\left\{{}\begin{matrix}x^2=36\\y^2=64\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{6;-6\right\}\\y\in\left\{8;-8\right\}\end{matrix}\right.\)
d: Ta có: 2x=3y
nên \(\dfrac{x}{3}=\dfrac{y}{2}\)
hay \(\dfrac{x}{21}=\dfrac{y}{14}\left(1\right)\)
Ta có: 5y=7z
nên \(\dfrac{y}{7}=\dfrac{z}{5}\)
hay \(\dfrac{y}{14}=\dfrac{z}{15}\left(2\right)\)
Từ (1), (2) suy ra \(\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{15}\)
hay \(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{75}\)
mà 3x-7y+5z=30
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{75}=\dfrac{3x-7y+5z}{63-98+75}=\dfrac{30}{40}=\dfrac{3}{4}\)
Do đó: \(\left\{{}\begin{matrix}x=\dfrac{63}{4}\\y=\dfrac{21}{2}\\z=\dfrac{45}{4}\end{matrix}\right.\)

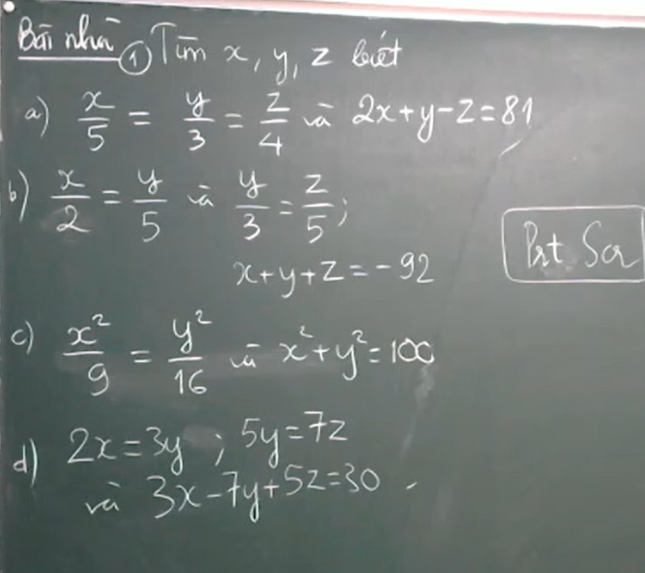





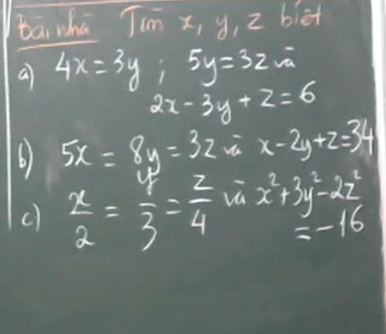

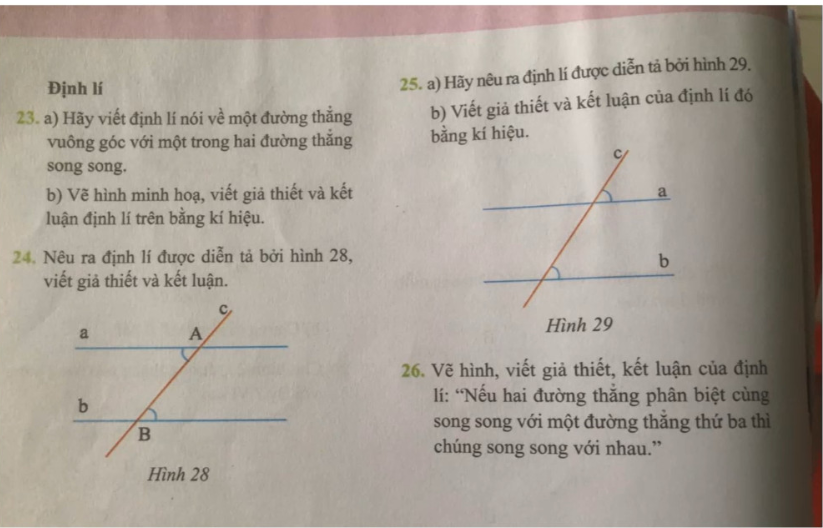








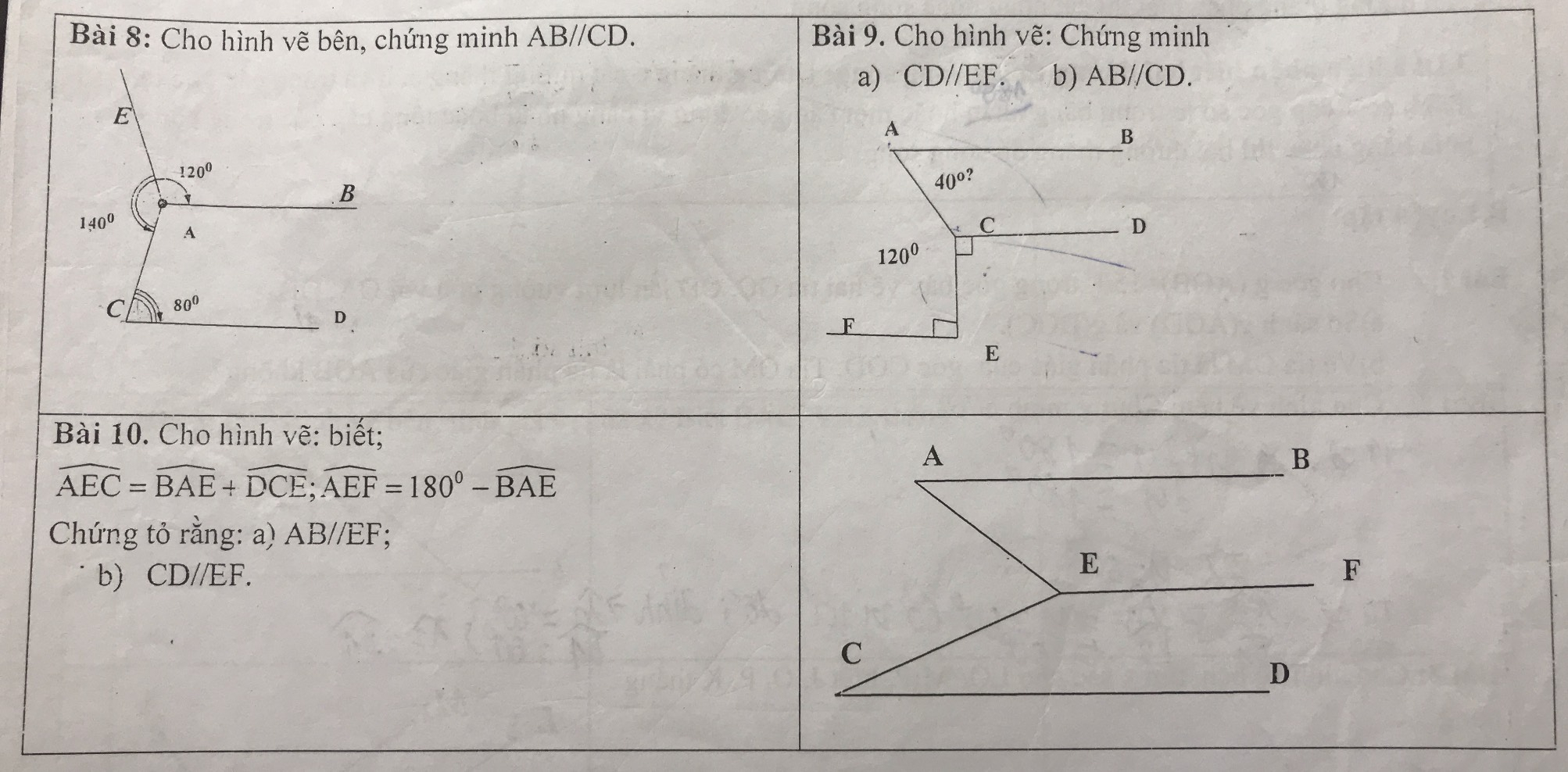 em bài 8,9,10 với ạ em gấp lắm rùi
em bài 8,9,10 với ạ em gấp lắm rùi 