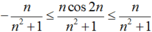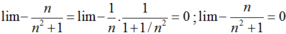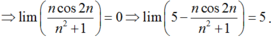Các câu hỏi tương tự
Cho hàm số f(n)
1
1
.
2
.
3
+
1
2
.
3
.
4
+
.
.
.
+
1
n
.
(
n
+
1
)...
Đọc tiếp
Cho hàm số f(n)= 1 1 . 2 . 3 + 1 2 . 3 . 4 + . . . + 1 n . ( n + 1 ) . ( n + 2 ) = n ( n + 3 ) 4 ( n + 1 ) ( n + 2 ) , n ∈ N * . Kết quả giới hạn lim ( 2 n 2 + 1 - 1 ) f ( n ) 5 n + 1 = a b ( b ∈ Z ) . Giá trị của a 2 + b 2 là
A.101
B.443
C.363
D.402
Cho hai số
3
n
và 8n với
n
∈
N
*
.a) So sánh
3
n
và 8n khi
n
1
,
2
,
3
,
4
,
5
.
b) Dự đoán kết quả tổng quát và chứng minh bằng phương pháp quy nạp
Đọc tiếp
Cho hai số 3 n và 8n với n ∈ N * .
a) So sánh 3 n và 8n khi n = 1 , 2 , 3 , 4 , 5 .
b) Dự đoán kết quả tổng quát và chứng minh bằng phương pháp quy nạp
1. hàm số y = 3cosx luôn nhận giá trị trong tập nào
2. tập xác định của hàm số y = cosx
3. tính giới hạn \(L=\lim\limits\dfrac{n^2-3n^3}{2n^3+5n-2}\)
4. tính giới hạn \(L=\lim\limits\left(3n^2+5n-3\right)\)
5. kết quả của giới hạn \(\lim\limits_{n\rightarrow+\infty}\left(n^3-2n^2+3n-4\right)\)
MỌI NGƯỜI GIÚP MÌNH MÔN TIN VỚI Ạ!Cho dãy số (a1, a2, a3, ..., an) là một hoán vị bất kỳ của tập hợp (1, 2, 3, ..., n). Dãy số (b1, b2, b3, ..., bn) gọi là nghịch thế của dãy a nếu bi là số phần tử đứng trước số i trong dãy a mà lớn hơn i.Ví dụ:Dãy a là: 3 2 5 7 1 4 6Dãy b là: 4 1 0 2 0 1 0a. Cho dãy a, hãy xây dựng chương trình tìm dãy b.b. Cho dãy b, xây dựng chương trình tìm dãy a.Dữ liệu vào: Trong file NGICH.INP với nội dung:-Dòng đầu tiên là số n (1 n 10 000).-Các dòng tiếp theo là n số...
Đọc tiếp
MỌI NGƯỜI GIÚP MÌNH MÔN TIN VỚI Ạ!
Cho dãy số (a1, a2, a3, ..., an) là một hoán vị bất kỳ của tập hợp (1, 2, 3, ..., n). Dãy số (b1, b2, b3, ..., bn) gọi là nghịch thế của dãy a nếu bi là số phần tử đứng trước số i trong dãy a mà lớn hơn i.
Ví dụ:
Dãy a là: 3 2 5 7 1 4 6
Dãy b là: 4 1 0 2 0 1 0
a. Cho dãy a, hãy xây dựng chương trình tìm dãy b.
b. Cho dãy b, xây dựng chương trình tìm dãy a.
Dữ liệu vào: Trong file NGICH.INP với nội dung:
-Dòng đầu tiên là số n (1 <= n <= 10 000).
-Các dòng tiếp theo là n số của dãy a, mỗi số cách nhau một dấu cách,
-Các dòng tiếp theo là n số của dãy b, mỗi số cách nhau bởi một dấu cách.
Dữ liệu ra: Trong file NGHICH.OUT với nội dung:
-N số đầu tiên là kết quả của câu a
-Tiếp đó là một dòng trống và sau đó là n số kết quả của câu b (nếu tìm được dãy a).
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh SB, SD và BC. Gọi E là giao điểm của mặt phẳng (MNP) với cạnh SA. Tính tỉ số SE SA . A. 1 4 . B. 1 2 . C. 1 3 . D. 3
Xét hai mệnh đề chứa biến P(n):
“
3
n
n
+
100
”
và Q(n):
2
n
n
với
n
∈
N
*
.a) Với n 1, 2, 3, 4, 5 thì P(n), Q(n) đúng hay sai?b) Với mọi n ∈ N* thì P(n), Q(n) đúng hay sai?
Đọc tiếp
Xét hai mệnh đề chứa biến P(n): “ 3 n < n + 100 ” và Q(n): " 2 n > n " với n ∈ N * .
a) Với n = 1, 2, 3, 4, 5 thì P(n), Q(n) đúng hay sai?
b) Với mọi n ∈ N* thì P(n), Q(n) đúng hay sai?
Dựa vào các công thức cộng đã học:
sin(a + b) = sina cosb + sinb cosa;
sin(a – b) = sina cosb - sinb cosa;
cos(a + b) = cosa cosb – sina sinb;
cos(a – b) = cosa cosb + sina sinb;
và kết quả cos π/4 = sinπ/4 = √2/2, hãy chứng minh rằng:
a) sinx + cosx = √2 cos(x - π/4);
b) sin x – cosx = √2 sin(x - π/4).
Số các giá trị nguyên của m để phương trình ( cos x + 1).(4.cos 2x – m.cos x) m.sin2x có đúng 2 nghiệm
x
∈
0
,
2
π
3
là: A. 3. B. 0. C. 2. D. 1.
Đọc tiếp
Số các giá trị nguyên của m để phương trình ( cos x + 1).(4.cos 2x – m.cos x) = m.sin2x có đúng 2 nghiệm x ∈ 0 , 2 π 3 là:
A. 3.
B. 0.
C. 2.
D. 1.
Tinh đao hàm của các hàm số
a (m + n/x^2)^4
b y =(3x-2)^11.(1-2x)^21
c y = căn của 2x-1/2x+1
d y = x . căn của x^2 +4