Lời giải:
\(I=\int (2\cos x+e^{\sin x})\cos xdx=2\int \cos ^2xdx+\int e^{\sin x}\cos xdx\)
\(=\int (\cos 2x+1)dx+\int e^{\sin x}d(\sin x)=\frac{\sin 2x}{2}+x+e^{\sin x}+c\)
Tính: \(\int\dfrac{ln\left(sinx+cosx\right)}{cos^2x}dx\)
Tìm nguyên hàm:
\(\int\dfrac{sin2x}{\left(2+sinx\right)^2}dx\)
Mấy bạn làm giúp mình câu nguyên hàm này với:
\(\int\dfrac{1}{sinx.sin\left(x+\dfrac{\pi}{6}\right)}dx\)
Tính các nguyên hàm.
a)\(\int\dfrac{2dx}{x^2-5x}=A\ln\left|x\right|+B\ln\left|x-5\right|+C\) . Tìm 2A-3B.
b)\(\int\dfrac{x^3-1}{x+1}\)dx=\(Ax^3-Bx^2+x+E\ln\left|x+1\right|+C\).Tính A-B+E
Giúp em bài này với ạ!
Giúp em giải bài này với ạ! Em cảm ơn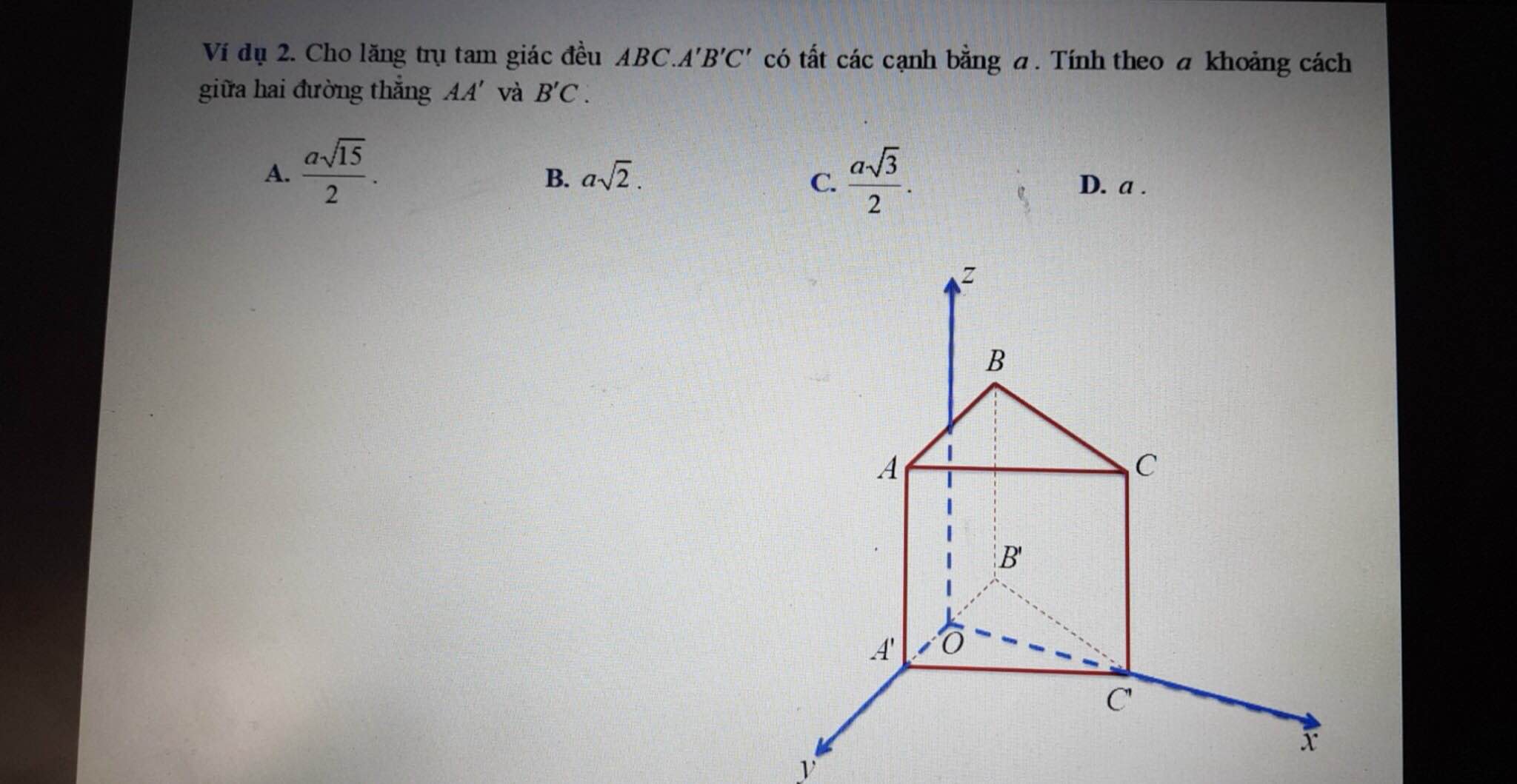
Giúp em giải bài này với ạ! Nhưng đừng tắt quá ạ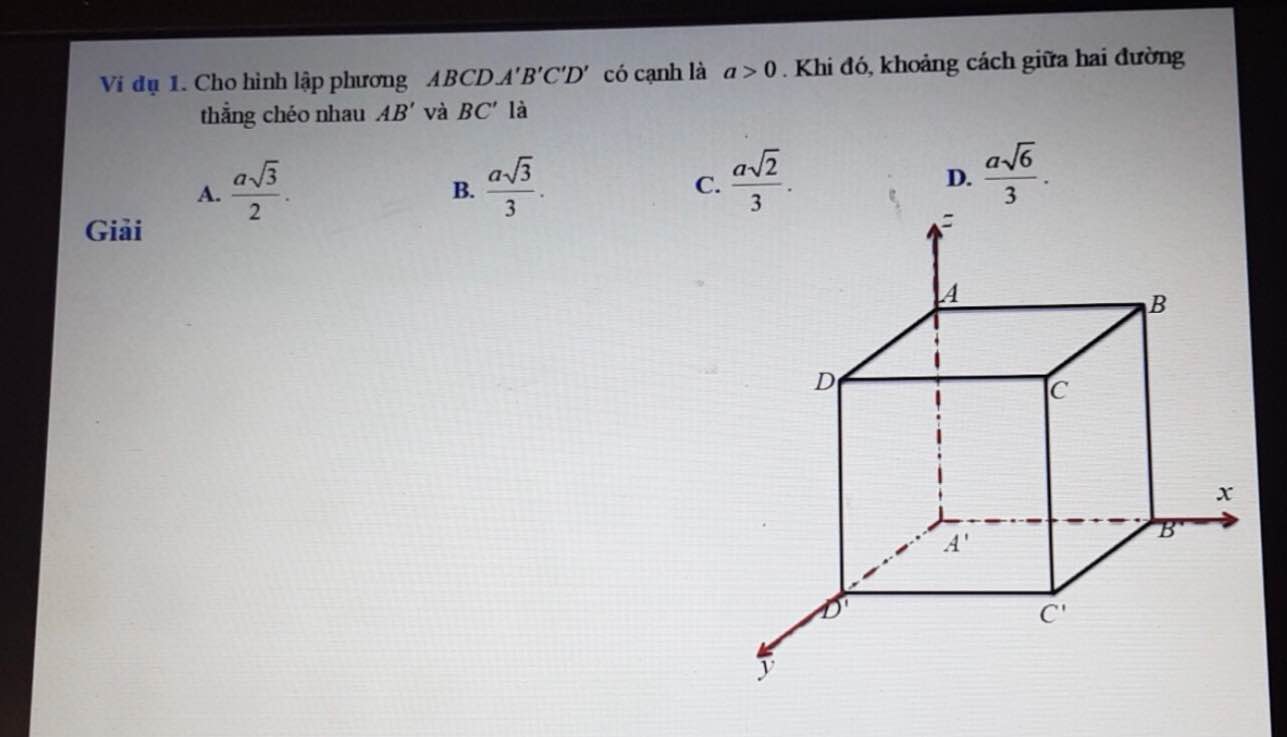
Mng giúp em bài này với ạ, em xin cảm ơn !😢
Thầy cô hướng dẫn giúp e bài này ạ, e cảm ơn ạ
Tìm nguyên hàm sau:
\(\int\dfrac{x^4}{\left(x^4-1\right)^3}\) và \(\int\dfrac{x^8}{\left(x^4-1\right)^3}\)
