Các câu hỏi tương tự
Cho số thực
a
≠
0
. Đặt
b
∫
−
a
a
1
2
a
+
x
e
x
d
x
. Tính
I
∫
0
2...
Đọc tiếp
Cho số thực a ≠ 0 . Đặt b = ∫ − a a 1 2 a + x e x d x . Tính I = ∫ 0 2 a e x 3 a − x d x theo a và b
A. I = b e a
B. I = b e a
C. I = b . e a
D. I = a e b
Cho số thực
a
≠
0
. Đặt
b
∫
-
a
a
1
(
2
a
+
x
)
.
e
x
d
x
. Tính
I
...
Đọc tiếp
Cho số thực a ≠ 0 . Đặt b = ∫ - a a 1 ( 2 a + x ) . e x d x . Tính I = ∫ 0 2 a e x 3 a - x d x theo a và b.
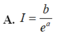
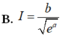
![]()
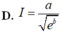
Hãy cho biết kết quả S của thuật toán nếu nhập n=4: Bước 1: Nhập n; Bước 2: Cho S=1, i=1; Bước 3: Kiểm tra nếu i<=n thì thực hiện bước 4, ngược lại thực hiện bước 6; Bước 4: S=S + i ; Bước 5: Tăng i lên 1 đơn vị và quay lại bước 3; Bước 6: In S và kết thúc chương trình.
Cho hàm số y f(x) xác định và liên tục trên
0
;
+
∞
sao cho
x
2
+
x
.
f
e
x
+
f
e
x
1
với mọi
x
∈
0
;
+...
Đọc tiếp
Cho hàm số y = f(x) xác định và liên tục trên 0 ; + ∞ sao cho x 2 + x . f e x + f e x = 1 với mọi x ∈ 0 ; + ∞ Tính tích phân I = ∫ e e ln x . f ( x ) x d x .
A. I = - 1 8 .
B. I = - 2 3 .
C. I = 1 12 .
D. I = 3 8 .
Gọi M và n lần lượt là gtln và gtnn của hàm số y= cos^2* x/3+ sin*x/3+1. Tính tổng M+n
Cho hàm số f(x) liên tục trên R. và thỏa mãn
∫
π
4
π
2
c
o
t
x
.
f
(
sin
2
x
)
d
x
∫
1
16
f
(
x
)...
Đọc tiếp
Cho hàm số f(x) liên tục trên R. và thỏa mãn ∫ π 4 π 2 c o t x . f ( sin 2 x ) d x = ∫ 1 16 f ( x ) x d x = 1 . Tính I= ∫ 1 8 1 f ( 4 x ) x d x .
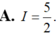
![]()
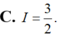
![]()
Cho hàm số f(x) liên tục trên
ℝ
và thoả mãn
∫
π
4
π
2
co
t
x
.
f
(
sin
2
x
)
d
x
∫
1
16
f
(
x...
Đọc tiếp
Cho hàm số f(x) liên tục trên ℝ và thoả mãn ∫ π 4 π 2 co t x . f ( sin 2 x ) d x = ∫ 1 16 f ( x ) x d x = 1
Tính tích phân I = ∫ 1 8 1 f ( π 4 x ) x d x
A. I = 3
B. I = 3/2
C. I = 2
D. I = 5/2
Cho
∫
-
π
π
cos
2
x
1
-
3
-
x
d
x
m
. Tính gía trị của
I
∫
-
π...
Đọc tiếp
Cho ∫ - π π cos 2 x 1 - 3 - x d x = m . Tính gía trị của I = ∫ - π π cos 2 x 1 + 3 x d x .
A. π - m
B. π 4 + m
C. π + m
D. π 4 - m
Cho tích phân
I
∫
1
2
3
d
x
x
+
1
2
x
+
3
. Đặt
t
2
x
+
3...
Đọc tiếp
Cho tích phân I = ∫ 1 2 3 d x x + 1 2 x + 3 . Đặt t = 2 x + 3 ta được I = ∫ 2 3 m t 2 + n d t (với m , n ∈ ℤ ). Tính T = 3m + n
A. T = 7.
B. T = 2.
C. T = 4.
D. T = 5.
Tính tích phân
I
∫
-
1
a
x
2
-
x
d
x
ta được kết quả I
11
6
, khi đó ta có: A. a 1. B. a 2. C. a 3. D. a 4.
Đọc tiếp
Tính tích phân I = ∫ - 1 a x 2 - x d x ta được kết quả I = 11 6 , khi đó ta có:
A. a = 1.
B. a = 2.
C. a = 3.
D. a = 4.





