Chọn D.
Tính I = ∫ 1 2 3 d x x + 1 2 x + 3
Đặt t = 2 x + 3 ⇒ t 2 = 2 x + 3 ⇒ 2 t d t = 2 d x x = t 2 - 3 2 ⇒ d x = t d t x + 1 = t 2 - 1 2
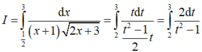
Vậy: m = 2, n = -1, T = 3.2 - 1 = 5.
Chọn D.
Tính I = ∫ 1 2 3 d x x + 1 2 x + 3
Đặt t = 2 x + 3 ⇒ t 2 = 2 x + 3 ⇒ 2 t d t = 2 d x x = t 2 - 3 2 ⇒ d x = t d t x + 1 = t 2 - 1 2
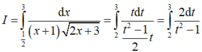
Vậy: m = 2, n = -1, T = 3.2 - 1 = 5.
Trong không gian OxyzOxyz cho hai điểm A(2;4;3)A(2;4;3) và B(2;7;1)B(2;7;1). Trong các phương trình dưới đây, phương trình nào là phương trình tham số của đường thẳng ABAB? (với t\in \Rt∈R)
A,\left\{{}\begin{matrix}x=2+2t\\y=7+4t\\z=1+3t\end{matrix}\right.⎩⎪⎨⎪⎧x=2+2ty=7+4tz=1+3t
B,\left\{{}\begin{matrix}x=4\\y=3+3t\\z=2-2t\end{matrix}\right.⎩⎪⎨⎪⎧x=4y=3+3tz=2−2t
c,\left\{{}\begin{matrix}x=2\\y=4-3t\\z=3+2t\end{matrix}\right.⎩⎪⎨⎪⎧x=2y=4−3tz=3+2t
d,\left\{{}\begin{matrix}x=2+2t\\y=4+7t\\z=3+t\end{matrix}\right.⎩⎪⎨⎪⎧x=2+2ty=4+7tz=3+t
Xét vị trí tương đối các cặp đường thẳng d và d' cho bởi các phương trình sau: a ) d : x = - 3 + 2 t y = - 2 + 3 t z = 6 + 4 t d ' : x = 5 + t ' y = - 1 - 4 t ' z = 20 + t '
b ) d : x = 1 + t y = 2 + t z = 3 - t d ' : x = 1 + 2 t ' y = - 1 + 2 t z = 2 - 2 t '
Cho A (1; 4; 2), B (-1; 2; 4), đường thẳng d : x = 5 - 4 t y = 2 + 2 t z = 4 + t và điểm M thuộc d. Tìm giá trị nhỏ nhất của diện tích tam giác AMB
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d: x = 1 + t y = 2 + 3 t z = 3 - t và d': x = 2 - 2 t ' y = - 2 - t ' z = 1 + 3 t ' . Tìm tọa độ M giao điểm của d và d'.
![]()
![]()
![]()
![]()
Cho hai đường thẳng d, d' và M(2; -1; 0)
d: x = 3 + t y = 1 - t z = 2 t , d': x = 1 + t ' y = 2 t ' z = - 1 + t '
Tìm tọa độ điểm A trên d và điểm B trên d' để M, A, B thẳng hàng.
Từ phương trình ( 3 + 2 2 ) x - 2 ( 2 - 1 ) x = 3 đặt t = ( 2 - 1 ) x ta thu được phương trình nào sau đây?
A. t 3 - 3 t - 2 = 0
B. 2 t 3 + 3 t 2 - 1 = 0
C. 2 t 3 + 3 t - 1 = 0
D. 2 t 2 + 3 t - 1 = 0
Trong không gian (Oxy) cho tam giác ABC có A (2;3;3), phương trình đường trung tuyến kẻ từ B là x - 3 - 1 = y - 3 2 = z - 2 - 1 , phương trình đường phân giác trong góc C là x - 2 2 = y - 4 - 1 = z - 2 - 1 . Biết rằng u → = m ; n ; - 1 là một véc tơ chỉ phương của đường thẳng AB. Tính giá trị biểu thức T=m²+n².
A. T=1
B. T=5
C. T=2
D. T=10
Xét tích phân I=\(\int\limits^{\dfrac{\pi}{2}}_0\dfrac{sin2x}{\sqrt{1+cosx}}dx\). Nếu đặt t=\(\sqrt{1+cosx}\), khẳng định nào dưới đây là đúng?
A. I= \(\int\limits^1_{\sqrt{2}}\dfrac{4t^3-4t}{t}dt\)
B. I= \(\int\limits^1_{\sqrt{2}}\dfrac{-4t^3+4t}{t}dt\)
C. I= \(4\int\limits^{\sqrt{2}}_1\left(t^2-1\right)dt\)
D. I= \(-4\int\limits^{\sqrt{2}}_1\left(t^2-1\right)dt\)
Tính các tích phân sau: ∫ - 3 2 d x x + 7 + 3 (đặt t = x + 7 hoặc t = x + 7 + 3)