Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Xác định giá trị a, b, c để hàm số
F
(
x
)
(
a
x
2
+
b
x
+
c
)
e
-
x
là một nguyên hàm của
f
(
x
)
(
x
2
-
3
x
+
2
)
e...
Đọc tiếp
Xác định giá trị a, b, c để hàm số F ( x ) = ( a x 2 + b x + c ) e - x là một nguyên hàm của f ( x ) = ( x 2 - 3 x + 2 ) e - x
A. a = -1; b = 1; c = -1
B. a = -1; b = -5; c = -7
C. a = 1; b = -3; c = 2
D. a = 1; b = -1; c = 1
Biết
F
(
x
)
(
a
x
2
+
b
x
+
c
)
e
-
x
là một nguyên hàm của hàm số
f
(
x
)
(
2
x
2
-
5
x
+
2
)
e
-...
Đọc tiếp
Biết F ( x ) = ( a x 2 + b x + c ) e - x là một nguyên hàm của hàm số f ( x ) = ( 2 x 2 - 5 x + 2 ) e - x trên R. Giá trị của biểu thức f(F(0)) bằng
A. 9e
B. 3e
C. 20 e 2
D. - 1 e
Đạo hàm của hàm số
y
x
+
2
x
-
1
ln
(
x
+
2
)
là A.
y
2
x
log
(...
Đọc tiếp
Đạo hàm của hàm số y = x + 2 x - 1 ln ( x + 2 ) là
A. y ' = 2 x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
B. y ' = x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
C. y ' = 2 x log ( 2 x - 1 ) + 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
D. y ' = - 2 x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
Cho hàm số f(x)=ln2018-ln(x+1 / x).Tính S=f’(1)+f’(2)+f’(3)+…+f’(2017)
A. 4035 2018
B. 2017
C. 2016 2017
D. 2017 2018
Cho hàm số yf(x) xác định và liên tục trên [1;e] thỏa mãn
xf
(
x
)
x
[
f
(
x
)
]
2
+
3
f
(
x
)
+
4
x
và f(1) -3. Tính f(e). A.
5
2
e
B. -...
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên [1;e] thỏa mãn xf ' ( x ) = x [ f ( x ) ] 2 + 3 f ( x ) + 4 x và f(1) = -3. Tính f(e).
A. 5 2 e
B. - 5 2
C. - 5 2 e
D. 5 2
Cho hàm số f(x) liên tục trong đoạn [1;e], biết
∫
1
e
f
(
x
)
x
d
x
1
, f(e) 2. Tích phân
∫
1
e...
Đọc tiếp
Cho hàm số f(x) liên tục trong đoạn [1;e], biết ∫ 1 e f ( x ) x d x = 1 , f(e) = 2. Tích phân ∫ 1 e f ' ( x ) ln x d x = ?
A. 1
B. 0
C. 2
D. 3
Cho hàm số yf(x) có đạo hàm liên tục trên R. Biết f(1)e và
(
x
+
2
)
f
(
x
)
x
f
(
x
)
-
x
3
, với mọi x thuộc R. Tính f(2). A.
4
e
2
-
4
e
+
4
B.
4...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên R. Biết f(1)=e và ( x + 2 ) f ( x ) = x f ' ( x ) - x 3 , với mọi x thuộc R. Tính f(2).
A. 4 e 2 - 4 e + 4
B. 4 e 2 - 2 e + 1
C. 2 e 3 - 2 e + 2
D. 4 e 2 + 4 e - 4
Một nguyên hàm F(x) của hàm số
f
(
x
)
e
-
x
+
e
x
2
thỏa mãn F(0) 1 là
Đọc tiếp
Một nguyên hàm F(x) của hàm số f ( x ) = e - x + e x 2 thỏa mãn F(0) = 1 là
![]()
![]()
![]()
![]()
Cho hàm số f(x) thỏa mãn
f
x
+
f
x
e
-
x
,
∀
x
∈
ℝ
và f(0) 2. Tất cả các nguyên hàm của
f
x
e
2
x
là A.
x
-
2...
Đọc tiếp
Cho hàm số f(x) thỏa mãn f x + f ' x = e - x , ∀ x ∈ ℝ và f(0) = 2. Tất cả các nguyên hàm của f x e 2 x là
A. x - 2 e x + e x + C
B. x + 2 e x + e x + C
C. x - 1 e x + C
D. x + 1 e x + C
Cho hàm số y f(x). Hàm số
y
f
x
có đồ thị như hình bên. Biết f(-1) 1,
f
-
1
e
2
. Bất phương trình f(x) ln(-x) + m đúng với mọi
x
∈
-
1
;
-
1
e
...
Đọc tiếp
Cho hàm số y = f(x). Hàm số y = f ' x có đồ thị như hình bên. Biết f(-1) = 1, f - 1 e = 2 . Bất phương trình f(x) < ln(-x) + m đúng với mọi x ∈ - 1 ; - 1 e khi và chỉ khi
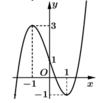
A. m > 2
B. m ≥ 2
C. m > 3
D. m ≥ 3




