Bai 1:
a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
\(\hat{AOM}=\hat{BOM}\)
Do đó: ΔOAM=ΔOBM
b: ΔOAM=ΔOBM
=>MA=MB
Bài 2:
a: Xét ΔHDB vuông tại D và ΔHEC vuông tại E có
HD=HE
\(\hat{DHB}=\hat{EHC}\) (hai góc đối đỉnh)
Do đó: ΔHDB=ΔHEC
b: ΔHDB=ΔHEC
=>\(\hat{HBD}=\hat{HCE}\)
Bài 3:
Xét ΔBAD và ΔBED có
BA=BE
\(\hat{ABD}=\hat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
=>DA=DE
BÀi 4:
a: TA có: \(BE=EC=\frac{BC}{2}\)
\(BA=\frac{BC}{2}\)
Do đó: BE=EC=BA
Xét ΔBAD và ΔBED có
BA=BE
\(\hat{ABD}=\hat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
=>\(\hat{BDA}=\hat{BDE}\)
=>DB là phân giác của góc ADE
b: ΔBAD=ΔBED
=>\(\hat{BAD}=\hat{BED}\)
=>\(\hat{BED}=90^0\)
=>DE⊥BC tại E
Xét ΔDBC có
DE là đường cao
DE là đường trung tuyến
Do đó: ΔDBC cân tại D
=>DB=DC
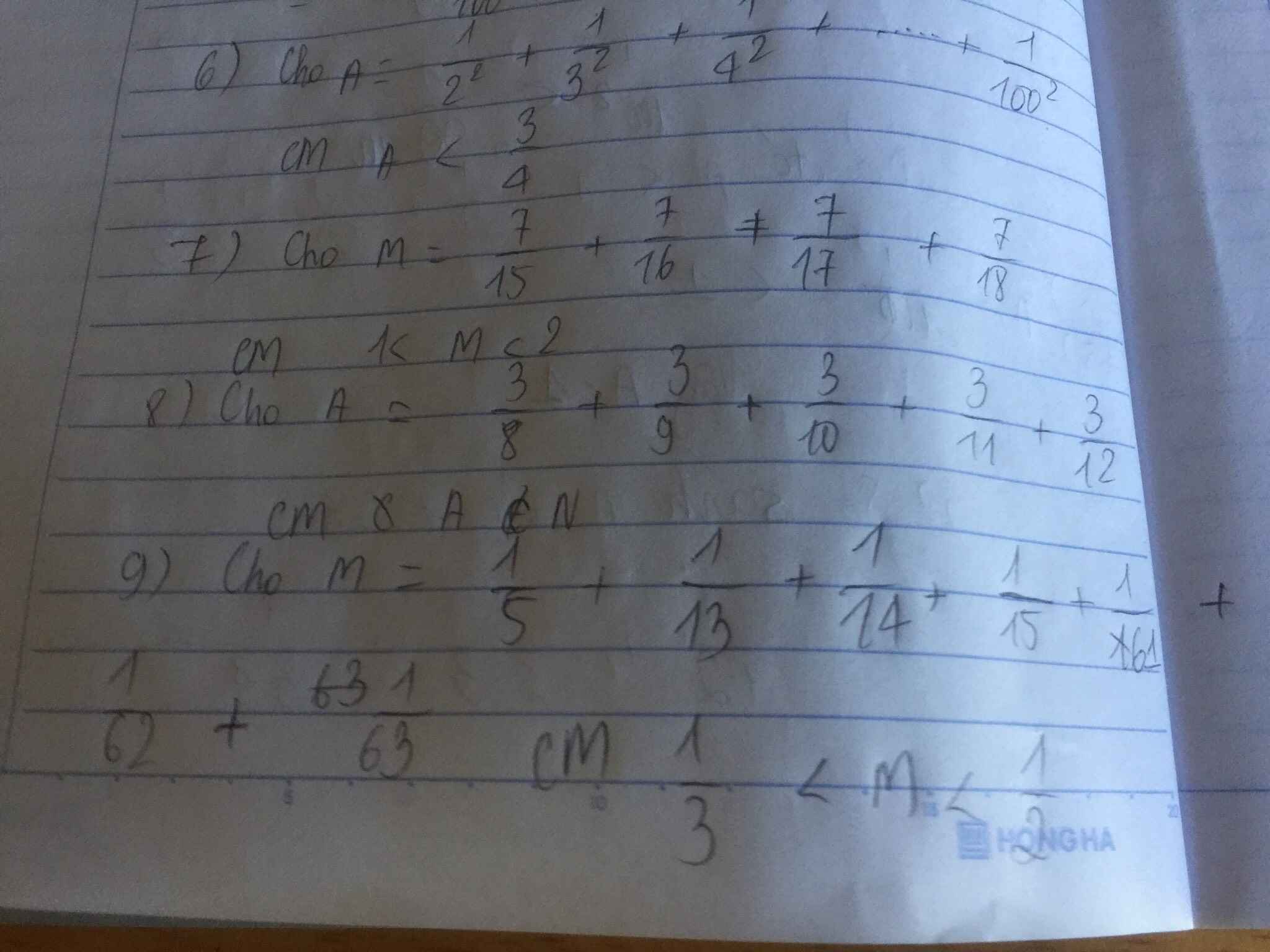
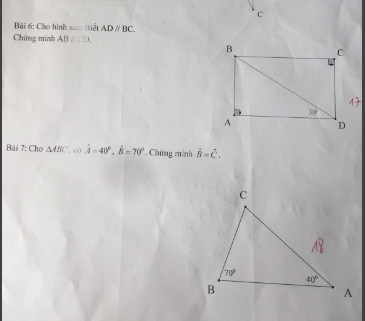mik cần gấp. GIẢI CỤ THỂ HỘ MIK VS Ạ
Giải hộ mik vs 
