Kẻ A M ⊥ B C và S H ⊥ A M , khi đó ∆ S H M vuông cân tại H. Suy ra H M = H S = h ; A M = 3 h
Vậy S = 9 3 4 h 2
Đáp án D
Kẻ A M ⊥ B C và S H ⊥ A M , khi đó ∆ S H M vuông cân tại H. Suy ra H M = H S = h ; A M = 3 h
Vậy S = 9 3 4 h 2
Đáp án D
Cho hình nón xoay có đường cao h = 4, bán kính đáy r = 3. Mặt phẳng (P) đi qua đỉnh của hình nón nhưng không qua trục của hình nón và cắt hình nón theo giao tuyến là một tam giác cân có độ dài cạnh đáy bằng 2. Tính diện tích S của thiết diện được tạo ra.
A. S = 91
B. S = 2 3
C. S = 19
D. S = 2 6
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S trên đáy là điểm H trên cạnh AC sao cho A H = 2 3 A C đường thẳng SB tạo với mặt phẳng đáy một góc 45 ° . Tính thể tích V của khối chóp S.ABC.
A. V = a 3 15 36
B. V = a 3 21 36
C. V = a 3 3 18
D. V = a 3 3 36
Cho hình chóp S.ABC có AB = 2a, AC = 4a, BC = 3a. Gọi H là hình chiếu của S nằm trong tam giác ABC. Các mặt bên tạo với đáy một góc 45 ° . Tính thể tích khối chóp S.ABC.
A. V = 15 a 3 6 .
B. V = 3 15 a 3 4 .
C. V = 15 a 3 8 .
D. V = 5 a 3 8 .
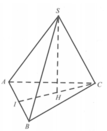
Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng a, gọi I là trung điểm của AB, hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của CI, góc giữa SA và mặt đáy bằng 45 ° (tham khảo hình vẽ bên dưới). Khoảng cách giữa 2 đường thẳng SA và CI bằng:
A. a 21 14
B. a 77 22
C. a 14 8
D. a 21 7
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy (ABC). Gọi H là hình chiếu vuông góc của A lên SC. Biết . Thể tích của khối chóp S.ABC bằng
A. 3 2
B. 3 4
C. 3 6
D. 3 12
Một hình trụ có chiều cao h=2, bán kính đáy r=3. Một mặt phẳng (P) không vuông góc với đáy của hình trụ, lần lượt cắt hai đáy theo các đoạn giao tuyến AB và CD sao cho tứ giác ABCD là hình vuông. Tính diện tích S của hình vuông ABCD
A. S=12ᴨ
B. S=12
C. S=20
D. S=20ᴨ
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy (ABC). Gọi H là hình chiếu vuông góc của A lên SC. Biết V S . A B H V S . A B C = 16 9 . Thể tích của khối chóp S.ABC bằng
A. 3 2
B. 3 4
C. 3 6
D. 3 12
Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh bằng a 2 . Tam giác (SAD) cân tại S và mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích khối chóp S.ABCD bằng 4 3 a 3 . Tính khoảng cách h từ B đến mặt phẳng (SCD).
A. h = 2 3 a
B. h = 4 3 a
C. h = 8 3 a
D. h = 3 4 a
Cho hình chóp A.BCD có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A trên mặt phẳng đáy là trung điểm H của CD. Cắt hình chóp bởi mặt phẳng ( α ) song song với AB và CD. Tính diện tích S của thiết diện thu được, biết d ( B , ( α ) ) = a 2 , A B = a 2
A. S = 4 a 15 ( a 15 + 2 a 2 )
B. S = 4 a 15 ( a 15 + a 2 )
C. S = 4 a 15 ( a 15 - 2 a 2 )
D. S = 4 a 15 ( a 15 - a 2 )