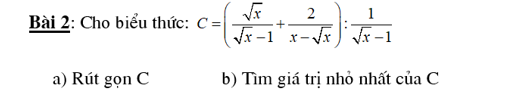Bài 4: Bổ sung đề: tia OM cắt (O) tại D
a: ΔOBC cân tại O
mà OD là đường cao
nên OD là phân giác của góc BOC
=>\(\hat{BOD}=\hat{COD}\left(3\right)\)
Xét (O) có
\(\hat{BAD}\) là góc nội tiếp chắn cung BD
=>\(\hat{BAD}=\frac12\cdot\hat{BOD}\left(1\right)\)
Xét (O) có \(\hat{CAD}\) là góc nội tiếp chắn cung CD
=>\(\hat{CAD}=\frac12\cdot\hat{COD}\left(2\right)\)
Từ (1),(2) suy ra \(\hat{BAD}=\hat{CAD}\)
b: Xét (O) có
ΔADE nội tiếp
DE là đường kính
Do đó: ΔADE vuông tại A
=>AE⊥DA
Xét ΔBAC có
AD là đường phân giác trong
AD⊥AE tại A
Do đó: AE là phân giác ngoài của ΔABC
Bài 5:
Ta có: \(\hat{MED}+\hat{MOC}=90^0\) (ΔEMO vuông tại M)
\(\hat{MOE}+\hat{MOA}=\hat{COA}=90^0\)
Do đó: \(\hat{MED}=\hat{MOA}\left(1\right)\)
Xét (O) có
\(\hat{MBA}\) là góc nội tiếp chắn cung MA
Do đó: \(\hat{MOA}=2\cdot\hat{MBA}\left(2\right)\)
Từ (1),(2) suy ra \(\hat{MED}=2\cdot\hat{MBA}\)
Bài 6:
a: Xét (O) có
\(\hat{CAM};\hat{CBM}\) là các góc nội tiếp chắn cung CM
Do đó: \(\hat{CAM}=\hat{CBM}\)
C là điểm chính giữa của cung AB
=>CA=CB
Xét ΔCAN và ΔCBM có
CA=CB
\(\hat{CAN}=\hat{CBM}\)
AN=BM
Do đó: ΔCAN=ΔCBM
b: ΔCAN=ΔCBM
=>CN=CM
Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
ΔCAN=ΔCBM
=>\(\hat{ACN}=\hat{BCM}\)
mà \(\hat{ACN}+\hat{BCN}=\hat{BCA}=90^0\)
nên \(\hat{BCM}+\hat{BCN}=90^0\)
=>\(\hat{MCN}=90^0\)
Xét ΔMCN có MC=CN và \(\hat{MCN}=90^0\)
nên ΔMCN vuông cân tại M
c:
Xét tứ giác ADCM có DC//AM
nên ADCM là hình thang
=>\(\hat{ADC}+\hat{DAM}=180^0\)
mà \(\hat{ADC}+\hat{AMC}=180^0\) (ADCM là hình thang cân)
nên \(\hat{DAM}=\hat{CMA}\)
=>DCMA là hình thang cân
=>DA=CM
Ta có: CM=CN
CM=AD
Do đó: CN=AD
Xét (O) có \(\hat{CMA}\) là góc nội tiếp chắn cung CA
=>\(\hat{CMA}=\frac12\cdot\hat{COA}=\frac12\cdot90^0=45^0\)
CDAM là hình thang cân
=>\(\hat{DAM}=\hat{CMA}=45^0\)
mà \(\hat{CMN}=\hat{CNM}\left(=45^0\right)\)
nên \(\hat{DAM}=\hat{CNM}\)
=>CN//AD
Xét tứ giác ANCD có
CN//AD
CN=AD
Do đó: ANCD là hình bình hành
Bài 7:
a: Xét (O) có
\(\hat{AMB};\hat{ACB}\) là các góc nội tiếp chắn cung AB
Do đó: \(\hat{AMB}=\hat{ACB}\)
mà \(\hat{ACB}=\hat{ABN}\) (ΔABC cân tại A)
nên \(\hat{AMB}=\hat{ABN}\)
Xét ΔAMB và ΔABN có
\(\hat{AMB}=\hat{ABN}\)
góc MAB chung
Do đó: ΔAMB~ΔABN
=>\(\frac{AM}{AB}=\frac{AB}{AN}\)
=>\(AM\cdot AN=AB^2\)
b: Ta có: \(AM\cdot AN=AB^2\)
mà AB=AC
nên \(AM\cdot AN=AC^2\)
=>\(\frac{AM}{AC}=\frac{AC}{AN}\)
Xét ΔAMC và ΔACN có
\(\frac{AM}{AC}=\frac{AC}{AN}\)
góc MAC chung
Do đó: ΔACM~ΔANC
=>\(\hat{ACM}=\hat{ANC}\)
Bài 3:
a: M là điểm chính giữa của cung AC
=>sđ cung MA=sđ cung MC
Xét (O) có
\(\hat{ABM}\) là góc nội tiếp chắn cung MA
\(\hat{CBM}\) là góc nội tiếp chắn cung CM
sđ cung MA=sđ cung MC
Do đó: \(\hat{ABM}=\hat{CBM}\)
=>BM là phân giác của góc ABC
Xét ΔABC có
BM,CI là các đường phân giác
BM cắt CI tại I
Do đó: I là tâm đường tròn nội tiếp ΔABC
b: Xét ΔABC có
I là tâm đường tròn nội tiếp
Do đó: AI là phân giác của góc BAC
Xét (O) có
\(\hat{BAN}\) là góc nội tiếp chắn cung BN
\(\hat{CAN}\) là góc nội tiếp chắn cung CN
\(\hat{BAN}=\hat{CAN}\)
Do đó: sđ cung BN=sđ cung CN
=>NB=NC
=>N nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra ON là đường trung trực của BC
=>ON⊥BC







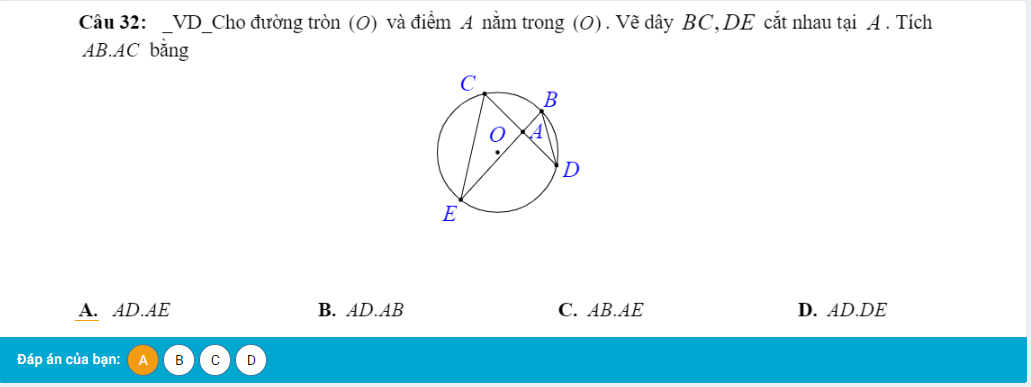



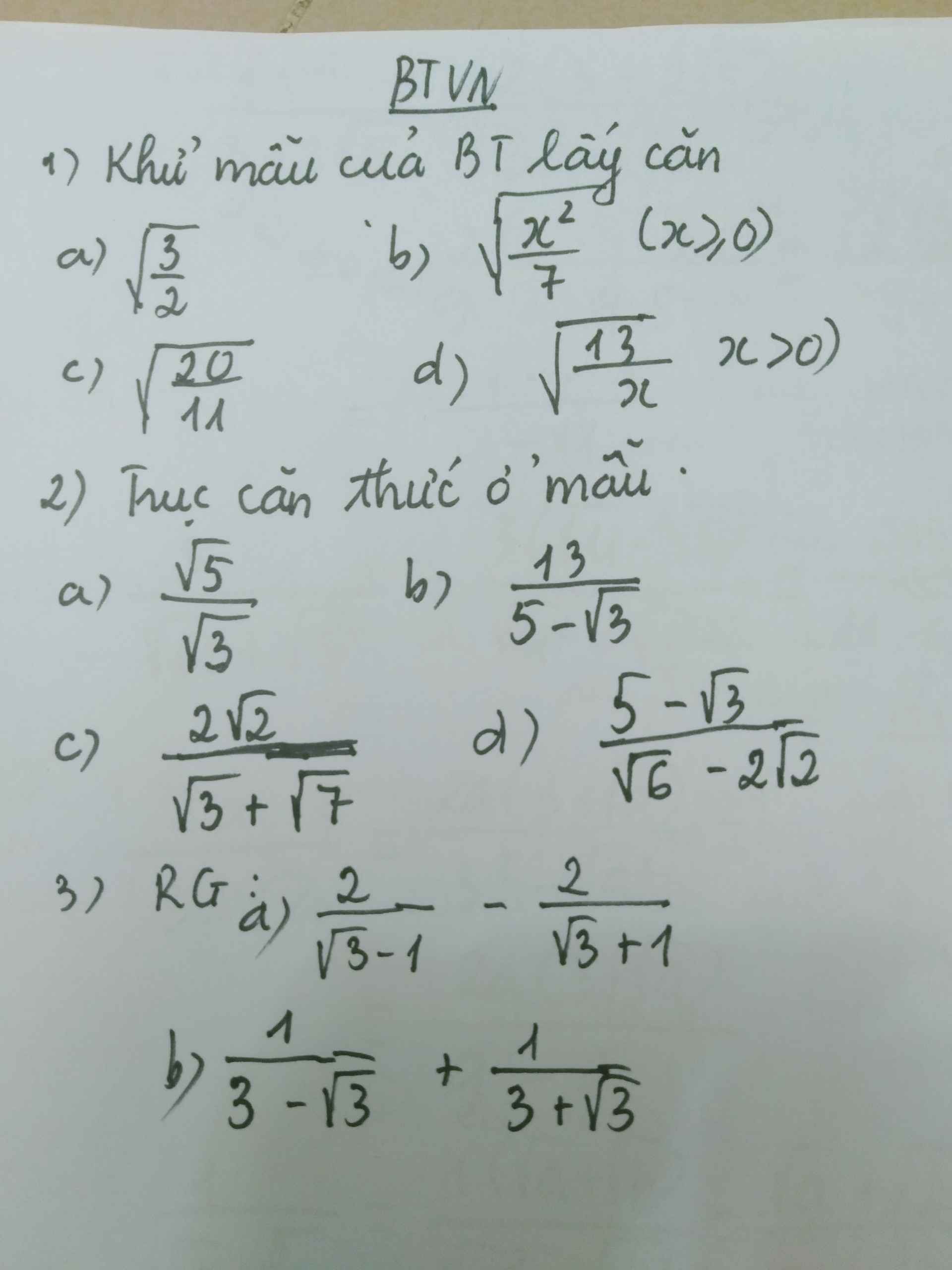


 HELP ME
HELP ME