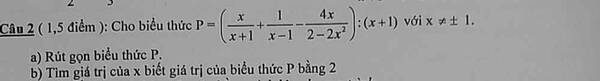Bài 2 :
\(a,\left(x+2\right)\left(x^2+3x-2\right)=2\left(x+2\right)x^2\)
\(\Leftrightarrow\left(x+2\right)\left(x^2+3x-2\right)-2x^2\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2+3x-2-2x^2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\-x^2+3x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\-x^2+x+2x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\-x\left(x-1\right)+2\left(x-1\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\\left(x-1\right)\left(-x+2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\\left[{}\begin{matrix}x-1=0\\-x+2=0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\end{matrix}\right.\)
Vậy \(S=\left\{-2;2;1\right\}\)
\(b,9x^2-\left(6x+2\right)\left(x-5\right)=1\)
\(\Leftrightarrow9x^2-\left(6x^2-30x+2x-10\right)-1=0\)
\(\Leftrightarrow9x^2-6x^2+30x-2x+10-1=0\)
\(\Leftrightarrow3x^2+28x+9=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=-9\end{matrix}\right.\)
Vậy \(S=\left\{-\dfrac{1}{3};-9\right\}\)
\(c,\dfrac{x}{3x-2}-\dfrac{x}{2+3x}=\dfrac{6x^2}{9x^2-4}\left(dkxd:x\ne\pm\dfrac{2}{3}\right)\)
\(\Leftrightarrow\dfrac{x}{3x-2}-\dfrac{x}{3x+2}-\dfrac{6x^2}{\left(3x-2\right)\left(3x+2\right)}=0\)
\(\Leftrightarrow\dfrac{x\left(3x+2\right)-x\left(3x-2\right)-6x^2}{\left(3x-2\right)\left(3x+2\right)}=0\)
\(\Leftrightarrow3x^2+2x-3x^2+2x-6x^2=0\)
\(\Leftrightarrow4x-6x^2=0\)
\(\Leftrightarrow-2x\left(-2+3x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-2x=0\\-2+3x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(tmdk\right)\\x=\dfrac{2}{3}\left(ktmdk\right)\end{matrix}\right.\)
Vậy \(S=\left\{0\right\}\)
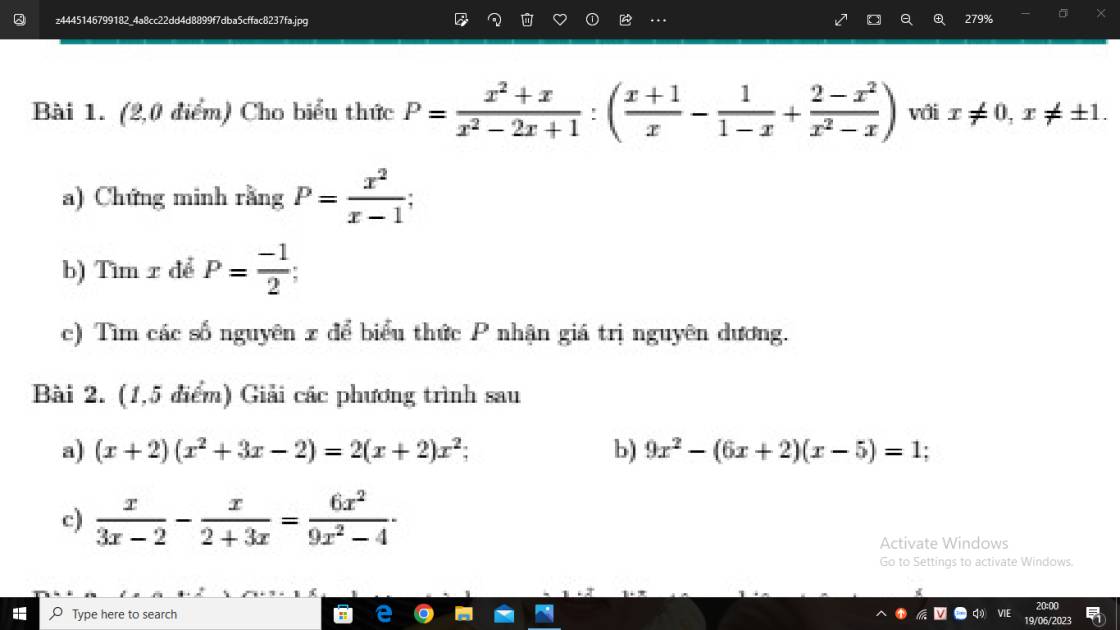
Bài 1 :
\(a,P=\dfrac{x^2+x}{x^2-2x+1}:\left(\dfrac{x+1}{x}-\dfrac{1}{1-x}+\dfrac{2-x^2}{x^2-x}\right)\left(dkxd:x\ne0,x\ne\pm1\right)\)
\(=\dfrac{x^2+x}{\left(x-1\right)^2}:\left(\dfrac{x+1}{x}+\dfrac{1}{x-1}+\dfrac{2-x^2}{x\left(x-1\right)}\right)\)
\(=\dfrac{x^2+x}{\left(x-1\right)^2}:\left(\dfrac{x^2-1+x+2-x^2}{x\left(x-1\right)}\right)\)
\(=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}.\dfrac{x\left(x-1\right)}{x+1}\)
\(=\dfrac{x^2}{x-1}\left(dpcm\right)\)
\(b,P=-\dfrac{1}{2}\Rightarrow\dfrac{x^2}{x-1}=-\dfrac{1}{2}\)
\(\Rightarrow2x^2=-\left(x-1\right)\)
\(\Rightarrow2x^2=-x+1\)
\(\Rightarrow2x^2+x-1=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-1\end{matrix}\right.\)
Vậy \(P=-\dfrac{1}{2}\) thì \(x=\dfrac{1}{2};x=-1\)
\(c,\) Để P nhận giá trị nguyên dương thì \(P\ge0\)
\(\Leftrightarrow\dfrac{x^2}{x-1}\ge0\Leftrightarrow x\ge0\)
1:
a: =>x^3+3x^2-2x+2x^2+6x-4=2x^3+4x^2
=>2x^3+4x^2=x^3+5x^2+4x-4
=>x^3-x^2-4x+4=0
=>(x-1)(x-2)(x+2)=0
=>x=1;x=2;x=-2
b: =>9x^2-6x^2+30x-2x+10=1
=>3x^2+28x+9=0
=>(x+9)(3x+1)=0
=>x=-1/3;x=-9
c: =>x(3x+2)-x(3x-2)=6x^2
=>6x^2=3x^2+2x-3x^2+2x=4x
=>2x(3x-2)=0
=>x=2/3(loại); x=0(nhận)










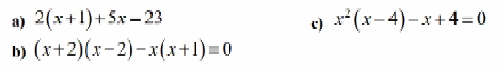




 help me
help me