Ta có:
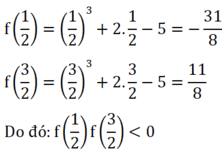
y = f(x) là hàm số đa thức liên tục trên R.
Do đó f(x)liên tục trên 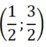
Từ đó suy ra, phương trình f(x) = 0 có ít nhất một nghiệm xo ∈ (0;2)
Ta có:
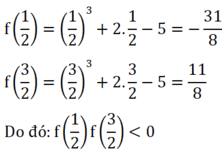
y = f(x) là hàm số đa thức liên tục trên R.
Do đó f(x)liên tục trên 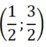
Từ đó suy ra, phương trình f(x) = 0 có ít nhất một nghiệm xo ∈ (0;2)
Cho hàm số y=f(x) liên tục trên đoạn [a; b]. Nếu f(a).f(b) > 0 thì phương trình f(x) = 0 có nghiệm hay không trong khoảng (a; b)? Cho ví dụ minh hoạ.
Cho 3 số thực a,b,c thỏa mãn a= -2b - 5c. CMR PT \(ax^2+bx+c=0\) có ít nhất 1 no thuộc khoảng (0;1)
cho phương trình ax^2+bx+c=0 với các số a,b,c là các số thực nghiệm khác 0 và thỏa mãn điều kiện a+b+2c=0. Chứng minh rằng phương trình trên luôn có nghiệm trên tập số thực
Bài 3: a) CMR phương trình sau có ít nhất hai nghiệm:
b) CMR phương trình sau có ít nhất một nghiệm âm:
c) Chứng minh phương trình có ít nhất một nghiệm .
giúp em với ạ
Cho \(f\left(x\right)=ax^2+bx+c\left(a,b,c\inℤ,a>0\right)\) sao cho phương trình \(f\left(x\right)=0\) có 2 nghiệm phân biệt thuộc \(\left(0;1\right)\). Tìm đa thức \(f\left(x\right)\) thỏa điều kiện trên mà \(a\) nhỏ nhất.
Cho hàm số f(x)liên tục trên đoạn [a ; b] và f(a) = b, f(b) = a, với 0 < a < b. Khi đó phương trình nào trong các phương trình sau đây luôn có nghiệm trên khoảng (a, b).
A. f x + x 2 = 0
B. f x + a = 0
C. f x - x = 0
D. f x + x = 0
Cho hàm số f ( x ) = x 3 + 8 x + 1 x - 2 . Phương trình f(x) = 0 có nghiệm hay không
a) trong khoảng (1; 3)?
b) trong khoảng (-3; 1)?
Nếu a+2b+3c=0 và a+c=0 thì phương trình asinx+bcos2x+c=0 có ít nhất 1 nghiệm trong khoảng (0;\(\frac{\pi}{6}\))
Gieo một con súc sắc cân đối và đồng nhất. giả sử con súc sắc xuất hiện mặt b chấm. Xét phương trình x 2 + b x + 2 = 0 . Tính xác suất sao cho:
a. Phương trình có nghiệm
b. Phương trình vô nghiệm
c. Phương tring có nghiệm nguyên.