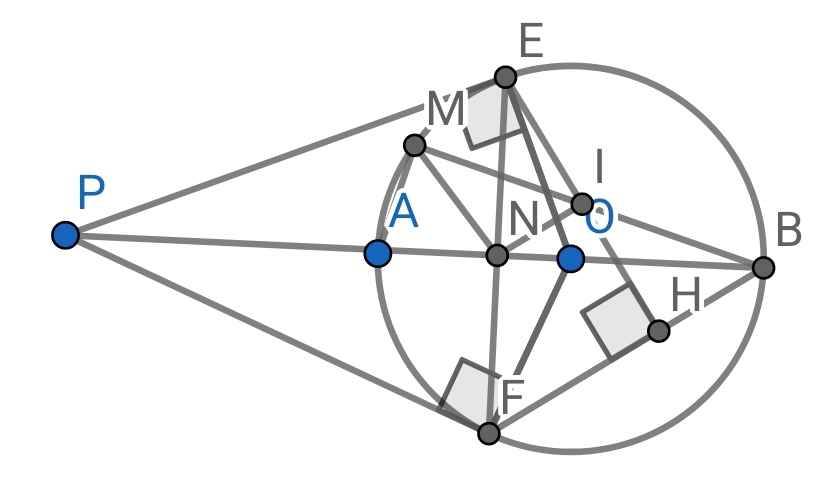
Hãy híu tui cíu tui vẽ cả hình ạ! Từ điểm P ở ngoài đường tròn (O) vẽ hai tiếp tuyến PE và PF. Tia PO cat dưong tròn ở A và B (A năm giữa P và O). Kẻ EH vuông góc với FB. Gọi I là trung điểm EH, Tia BI căt (O) tại điểm thứ hai M (M khác B), EF cắt AB tại N. Chứng minh a) NI // FB b) Tứ giác MEIN nội tiếp và EMN = 90.
a) Ta có:
PE = PF (tính chất hai tiếp tuyến cắt nhau)
⇒ P nằm trên đường trung trực của EF (1)
Lại có:
OE = OF (bán kính)
⇒ O nằm trên đường trung trực của EF (2)
Từ (1) và (2) ⇒ OP là đường trung trực của EF
Lại có:
N là giao điểm của EF và AB (gt)
⇒ N là giao điểm của EF và OP
⇒ N là trung điểm của EF
∆HEF có:
I là trung điểm của EH (gt)
N là trung điểm của EF (cmt)
⇒ NI là đường trung bình của ∆HEF
⇒ NI // FH
⇒ NI // FB
b) Do NI // FB (cmt)
⇒ ∠NIM = ∠FBM (đồng vị)
Mà ∠FBM = ∠FEM (hai góc nội tiếp cùng chắn cung FM của (O))
⇒ ∠NIM = ∠FEM
⇒ ∠NIM = ∠NEM
Tứ giác MEIN có:
∠NIM = ∠NEM (cmt)
⇒ I và E cùng nhìn NM dưới một góc bằng nhau
⇒ MEIN nội tiếp
Do NI // FB (cmt)
FB ⊥ EH (gt)
⇒ NI ⊥ EH
⇒ ∠NIE = 90⁰
Do MEIN nội tiếp (cmt)
⇒ ∠NIE + ∠EMN = 180⁰
⇒ ∠EMN = 180⁰ - ∠NIE
= 180⁰ - 90⁰
= 90⁰












