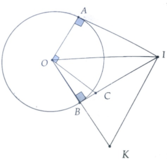
a, Chứng minh C là trực tâm của tam giác OIK. Từ đó suy ra KC ⊥ OI tại H
b, IA=12cm
Chứng minh ΔKOI cân tại K
Đặt KO = KI = x (x>0)
Có I K 2 = I B 2 + B K 2
Hay x 2 = 12 2 + x - 9 2
=> x = 12,5 => IK = 12,5cm
Đúng 0
Bình luận (1)
Các câu hỏi tương tự
Cho hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại I. Đường thẳng đi qua I và vuông góc với IA cắt OB tại K. Chứng minh
a) IK//OA
b) Tam giác IOK cân
giúp câu b vs ạ
Từ điểm A nằm ngoài đường tròn (O) , kẻ 2 tiếp tuyến AB , AC đến đường tròn (O) (B, C là 2 tiếp điểm )a) cm 4 điểm O,B,A,C cùng thuộc một đường tròn và BC vuông góc với OA tại Hb) kẻ đường kính CD của đường tròn (O) . CM : BD//OAc) Gọi E là trung điểm của BD , EH cắt OB tại M , đường thẳng qua E song song với AB cắt AD tại N . Các đường thẳng vuông góc với EM tại M và vuông góc với EM tại N cắt nhau tại I .Chứng minh : IO IAVẽ hình dùm tớ nhé !!!! THANKS CÁC CẬU NHIỀU LẮM !!!!! 3
Đọc tiếp
Từ điểm A nằm ngoài đường tròn (O) , kẻ 2 tiếp tuyến AB , AC đến đường tròn (O) (B, C là 2 tiếp điểm )
a) cm 4 điểm O,B,A,C cùng thuộc một đường tròn và BC vuông góc với OA tại H
b) kẻ đường kính CD của đường tròn (O) . CM : BD//OA
c) Gọi E là trung điểm của BD , EH cắt OB tại M , đường thẳng qua E song song với AB cắt AD tại N . Các đường thẳng vuông góc với EM tại M và vuông góc với EM tại N cắt nhau tại I .Chứng minh : IO = IA
Vẽ hình dùm tớ nhé !!!! THANKS CÁC CẬU NHIỀU LẮM !!!!! <3
Cho đường tròn tâm O đường kính AB = 10cm. Điểm I nằm giữa A và O sao cho OI = IA. Vẽ dây cung CD vuông góc với Oa tại I. Gọi H là trung điểm của IC. Qua H vẽ đường thẳng vuông góc với CO cắt CO tại M và cắt (O) tại E; F. Chúng minh rằng AB là tiếp tuyến của (C; CE).
Cho đường tròn tâm O đường kính AB = 10cm. Điểm I nằm giữa A và O sao cho OI = IA. Vẽ dây cung CD vuông góc với Oa tại I. Gọi H là trung điểm của IC. Qua H vẽ đường thẳng vuông góc với CO cắt CO tại M và cắt (O) tại E; F. Chúng minh rằng AB là tiếp tuyến của (C; CE).
cho đường tròn (O;R) và điểm A nằm ngoài đường tròn (O) sao cho OA=2R. vẽ tiếp tuyến AB với đường tròn (O). BH là đường cao của tam giác ABO, BH cắt (O) tại C.
a. CM: AC là tiếp tuyến của (O)
b. từ O vẽ đường thẳng vuông góc với OB cắt AC tại K. chứng minh KA=KO.
c. đoạn thẳng OA cắt (O) tại I. chứng minh KI là tiếp tuyến của đường tròn (O) và tính IK theo R
cho (O,R) lấy điểm A cách O một khoản bằng 2R . Kẻ tiếp tuyến AB và Ac với đường tròn ( B,C là các tiếp điểm ). Doạn thẳng OA cắt đường tròn (O) tại I . Đường thẳng qua O và vuông góc với OB cắt AC tại K.
a, chứng minh tam giác OAK cân tại K
b, đường thẳng KI cắt AB tại M. CM : KM là tiếp tuyến của (O)
c, tính chu vi tam giác AMK theo R
Cho (O;R) và dây AB, các tiếp tuyến tại A và B của ((O) cắt nhau tại C. Lấy điểm I trên dây AB sao cho IA>IB. Từ điểm I kẻ đường thẳng vuông góc với OI cắt AC tại E và cắt BC tại D. cm: góc IBO= góc IDO; b) OE=OD
cho đường tròn tâm o bán kính r lấy A sao cho AO=2r các tiếp tuyến AB, AC với đường tròn tâm O OA cắt O tại I đường thẳng đi qua O và vuông góc với OB cắt AC tại K a, chứng minh tam giác OAK cân tại K b, đường thẳng KI cắt AB tại m. chứng minh KM là tiếp tuyến của đường tròn tâm O c, tính chu vi tam giác AMK theo r
18 tháng 12 2023 lúc 14:57
Cho đường tròn (O;R) và điểm A nằm ngoài (O) sao cho OA = 2R, vẽ tiếp tuyến AB với (O). Gọi BH là đường cao ∆ABO, BH cắt (O) tại C.
a) Cm AC là tiếp tuyến (O)
b) Từ O vẽ đường vuông góc với OB cắt AC tại K. Cm KA = KO.
c) Đoạn OA cắt (O) tại I. Cm IK là tiếp tuyến (O), tính IK theo R.
d) AI cắt (O) tại điểm thứ hai D. Cm ∆AIC ~ ∆ACD từ đó suy ra tích AI × AD không đổi.