Chọn đáp án A.
Phương pháp: Tính giá trị biểu thức dạng ![]() là hai nghiệm phức của phương trình bậc hai
là hai nghiệm phức của phương trình bậc hai 
+ Giải phương trình bậc hai ra nghiệm ![]()
+ Đưa về dạng ![]()
+ Dùng công thức Moivre: ![]()
Cách giải
Phương trình bậc 2 đã cho có ![]()
![]() Có 2 nghiệm
Có 2 nghiệm

Chọn đáp án A.
Phương pháp: Tính giá trị biểu thức dạng ![]() là hai nghiệm phức của phương trình bậc hai
là hai nghiệm phức của phương trình bậc hai 
+ Giải phương trình bậc hai ra nghiệm ![]()
+ Đưa về dạng ![]()
+ Dùng công thức Moivre: ![]()
Cách giải
Phương trình bậc 2 đã cho có ![]()
![]() Có 2 nghiệm
Có 2 nghiệm

Gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - 2z + 2 = 0, (z ∈ ℂ ). Tính giá trị của biểu thức P = 2| z 1 + z 2 | + | z 1 - z 2 |
A. P = 6
B. P = 3
C. P = 2 2 + 2
D. P = 2 + 4
Gọi z 1 ; z 2 là hai nghiệm phức của phương trình 3 z 2 - z + 2 = 0 . Tính giá trị biểu thức T = z 1 2 + z 2 2 .
A. T = 2 3
B. T = 8 3
C. T = 4 3
D. T = - 11 9
Gọi z1; z2; z3; z4 là bốn nghiệm của phương trình ( z - 1 )( z + 2) ( z2 - 2z + 2) = 0 trên tập số phức, tính tổng: 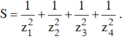
A. 2/5
B. 3/5
C. 5/4
D. 6/7
Gọi z 1 , z 2 là hai nghiệm phức của phương trình z 2 + 2z + 10 = 0. Tính giá trị của biểu thức A = | z 1 | 2 + | z 2 | 2
A. 15
B. 17
C. 19
D. 20
Gọi z 1 ; z 2 là hai nghiệm phức của phương trình z 2 - 2 z + 2 = 0 . Tính giá trị của biểu thức P = 2 z 1 + z 2 + z 1 - z 2 .
A. P = 6
B. P = 3
C. P = 2 2 + 2
D. 2 + 4
Gọi z 1 , z 2 là 2 nghiệm của phương trình 2 z 2 + z + 1 = 0 . Tính giá trị biểu thức A = z 1 2 + z 2 2
![]()
![]()
![]()
![]()
Gọi z 1 ; z 2 là 2 nghiệm của phương trình 2 z 2 + z + 1 = 0 . Tính giá trị biểu thức A = z 1 2 + z 2 2 .
A. 2
B. 1
C. 4
D. 3
Gọi z1, z2 lần lượt là hai nghiệm của phương trình z2 - (1 + 3i) z – 2 + 2i = 0 và thỏa mãn | z1| > | z2|. Tìm giá trị của biểu thức

A. 0,5
B. 1,5
C. 1
D. 2
Gọi z 1 và z 2 là hai nghiệm phức của phương trình z 2 + z + 1 = 0 . Tính giá trị của z 1 2017 + z 2 2017
A. ![]()
B. ![]()
C. ![]()
D. ![]()