Các câu hỏi tương tự
Gọi I là giao điểm hai đường tiệm cận của đồ thị hàm số y = 2 - x x - 1 . Tìm tọa độ của I
A. I(1;-1)
B. I(-1;-1)
C. I(-1;1)
D. I(1;1)
Cho hàm số
y
x
+
3
x
−
2
có đồ thị
C
. Gọi I là giao điểm của hai đường tiệm cận của
C
. Khi đó tọa độ của điểm I là A.
I
−
3
;
0
.
B. ...
Đọc tiếp
Cho hàm số y = x + 3 x − 2 có đồ thị C . Gọi I là giao điểm của hai đường tiệm cận của C . Khi đó tọa độ của điểm I là
A. I − 3 ; 0 .
B. I 1 ; 2 .
C. I 2 ; 1 .
D. I 0 ; − 3 2 .
Cho hàm số có đồ thị y = x − 2 x + 2 có đồ thị (C). Tìm tọa độ giao điểm I của hai đường tiệm cận của đồ thị (C)
A. I(-2;2)
B. I(-2;2)
C. I(2;1)
D. I(-2;1)
Gọi I là giao điểm của hai đường tiệm cận của đồ thị hàm số
y
2
x
-
3
x
+
1
.
Khi đó, điểm I nằm trên đường thẳng có phương trình A.
x
+
y
+
4
0
B.
2
x
-...
Đọc tiếp
Gọi I là giao điểm của hai đường tiệm cận của đồ thị hàm số y = 2 x - 3 x + 1 . Khi đó, điểm I nằm trên đường thẳng có phương trình
A. x + y + 4 = 0
B. 2 x - y + 4 = 0
C. x - y + 4 = 0
D. 2 x - y + 2 = 0
Cho hàm số
y
x
+
1
x
-
1
có đồ thị (C). Gọi I là giao điểm của hai tiệm cận, M là một điểm thuộc (C). Tiếp tuyến tại M của (C) cắt hai tiệm cận tại A và B. Phát biểu nào sau đây là sai? A. M là trung điểm của AB B. Diện tích tam giác IAB là một số không đổi C. Tích khoảng cách từ M đến hai tiệm cận là một số không đổi D. Tổng khoảng cách từ M đến hai tiệm cận là mộ...
Đọc tiếp
Cho hàm số y = x + 1 x - 1 có đồ thị (C). Gọi I là giao điểm của hai tiệm cận, M là một điểm thuộc (C). Tiếp tuyến tại M của (C) cắt hai tiệm cận tại A và B. Phát biểu nào sau đây là sai?
A. M là trung điểm của AB
B. Diện tích tam giác IAB là một số không đổi
C. Tích khoảng cách từ M đến hai tiệm cận là một số không đổi
D. Tổng khoảng cách từ M đến hai tiệm cận là một số không đổi
Cho hàm số
y
x
−
1
x
−
3
. Xét các mệnh đề sau:(1) Hàm số nghịch biến trên
D
ℝ
3
(2) Đồ thị hàm số có một tiệm cận đứng là x1, tiệm cận ngang là y3.(3) Hàm số đã cho không có cực trị(4) Đồ thị hàm số nhận giao điểm I(3;1) của hai đường tiệm cận làm tâm đối xứng...
Đọc tiếp
Cho hàm số y = x − 1 x − 3 . Xét các mệnh đề sau:
(1) Hàm số nghịch biến trên D = ℝ \ 3
(2) Đồ thị hàm số có một tiệm cận đứng là x=1, tiệm cận ngang là y=3.
(3) Hàm số đã cho không có cực trị
(4) Đồ thị hàm số nhận giao điểm I(3;1) của hai đường tiệm cận làm tâm đối xứng.
Chọn các mệnh đề đúng ?
A. (1), (3), (4)
B. (3), (4)
C. (2), (3), (4)
D. (1), (4)
Cho hàm số
y
2
x
-
1
2
x
-
2
có đồ thị (C). Gọi
M
x
0
;
y
0
(với
x
0
1
) là điểm thu...
Đọc tiếp
Cho hàm số y = 2 x - 1 2 x - 2 có đồ thị (C). Gọi M x 0 ; y 0 (với x 0 > 1 ) là điểm thuộc (C), biết tiếp tuyến của (C) tại M cắt tiệm cận đứng và tiệm cận ngang lần lượt tại A và B sao cho S ∆ O I B = 8 S ∆ O I A (trong đó O là gốc tọa độ, I là giao điểm hai tiệm cận). Giá trị của S = x 0 + 4 y 0 bằng
A. 8
B. 2
C. 17 4
D. 23 4
Cho hàm số
y
f
x
x
+
1
x
−
1
có đồ thị (C). Giả sử A, B là hai điểm nằm trên (C) đồng thời đối xứng nhau qua điểm I là giao điểm của hai đường tiệm cận của đồ thị (C). Dựng hình vuông AEBD . Tìm diện tích nhỏ nhất
S
min
của hình vuông đó. A....
Đọc tiếp
Cho hàm số y = f x = x + 1 x − 1 có đồ thị (C). Giả sử A, B là hai điểm nằm trên (C) đồng thời đối xứng nhau qua điểm I là giao điểm của hai đường tiệm cận của đồ thị (C). Dựng hình vuông AEBD . Tìm diện tích nhỏ nhất S min của hình vuông đó.
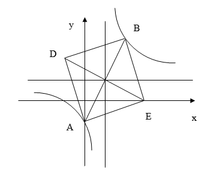
A. S min = 8 2
B. S min = 4 2
C. S min = 4
D. S min = 8
Cho hàm số
y
x
+
2
x
+
1
có đồ thị là
C
và
I
là giao của hai tiệm cận của
C
. Điểm
M
di chuyển trên
C
. Giá trị nhỏ nhất của độ dài đoạn
I
M
bằng A.
1
. B....
Đọc tiếp
Cho hàm số y = x + 2 x + 1 có đồ thị là C và I là giao của hai tiệm cận của C . Điểm M di chuyển trên C . Giá trị nhỏ nhất của độ dài đoạn I M bằng
A. 1 .
B. 2 .
C. 2 2 .
D. 6 .




