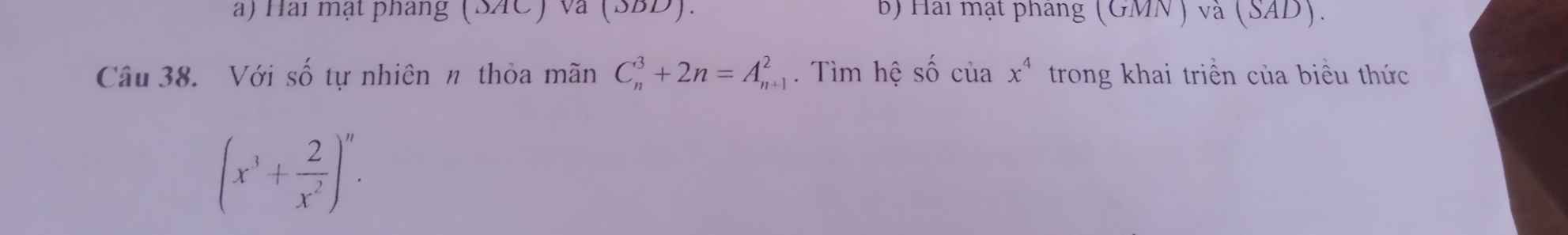1.
a. Đúng
Do E là trung điểm AB, F là trung điểm BC nên EF là đường trung bình tam giác ABC
⇒EF//AC
b. Sai
Do AB song song CD (ABCD là hbh) và S là 1 giao điểm của (SAB) và (SCD) nên giao tuyến của (SAB) và (SCD) là đường thẳng qua S và song song AB, CD
c. Đúng
Do AD song song BC (ABCD là hbh) và M thuộc AD nên M là 1 giao điểm của (SAD) và (MBC)
\(\) ⇒Giao tuyến của (SAD) và (MBC) là đường thẳng qua M và song song BC
d. Đúng
Lý do tương tự câu c, EF song song AC (theo cm câu a) và M là 1 điểm chung của (SAC) và (MEF)
3.
a. Đúng (giả thiết cho sẵn)
b. Sai
Do AB song song CD (gt) và (ICD) cắt SA, SB tại M, N nên \(MN=\left(SAB\right)\cap\left(ICD\right)\)
\(\rArr MN\Vert AB\Vert CD\)
Đặt \(SN=x.SB\)
O là trung điểm BD và I là trung điểm SO nên
\(\overrightarrow{SI}=\frac12\overrightarrow{SO}=\frac12\left(\frac12\overrightarrow{SB}+\frac12\overrightarrow{SD}\right)=\frac14\overrightarrow{SB}+\frac14\overrightarrow{SD}\)
\(\overrightarrow{DI}=\overrightarrow{DS}+\overrightarrow{SI}=-\overrightarrow{SD}+\frac14\overrightarrow{SB}+\frac14\overrightarrow{SD}=\frac14\overrightarrow{SB}-\frac34\overrightarrow{SD}\)
\(\overrightarrow{DN}=\overrightarrow{DS}+\overrightarrow{SN}=x.\overrightarrow{SB}-\overrightarrow{SD}\)
Do D, I, N thẳng hàng nên:
\(\frac{\frac14}{x}=\frac{-\frac34}{-1}\rArr x=\frac13\)
\(\Rightarrow SN=\frac13SB\)
c. Sai
Theo cm câu b ta có \(SN=\frac13SB\)
Mặt khác MN song song AB (theo cm câu b) nên theo định lý Thales:
\(\frac{MN}{AB}=\frac{SN}{SB}=\frac13\Rightarrow MN=\frac13AB=\frac{a}{3}\)
d. Sai
Theo gt ta có \(K\in CN\in\left(SBC\right)\)
\(K\in DM\in\left(SAD\right)\)
\(\Rightarrow K\in\left(SAD\right)\cap\left(SBC\right)\)
\(\Rightarrow SK=\left(SAD\right)\cap\left(SBC\right)\)
Mà SD song song BC (gt) nên \(SK\Vert BC\)
2.
a. Đúng
I là trung điểm AD, J là trung điểm AC nên IJ là đường trung bình tam giác ACD
\(\rArr IJ\Vert CD\)
b. Sai
Do IJ song song CD (cm câu a) và G là 1 điểm chung của (GIJ) và (BCD) nên giao tuyến của (GIJ) và (BCD) là đường thẳng qua G và song song CD
c. Sai
Theo câu b ta có MN song song CD
Mặt khác theo định lý Thales và tính chất trọng tâm ta có \(MN=\frac23CD\rArr MN=4\)
IJ là đtb tam giác ACD (cm câu a) nên \(IJ=\frac12CD=3\)
\(\rArr2IJ+3MN=2.3+3.4=18\)
d. Sai
Theo tính toán từ câu c ta có MN=4 và IJ=3 nên 3IJ+2MN=3.3+4.2=17