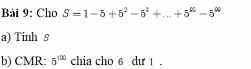\(B=\dfrac{6}{15.18}+\dfrac{6}{18.21}+\dfrac{6}{21.24}+...+\dfrac{6}{87.90}\)
\(=2\left(\dfrac{1}{15}-\dfrac{1}{18}+\dfrac{1}{18}-\dfrac{1}{21}+\dfrac{1}{21}-\dfrac{1}{24}+...+\dfrac{1}{87}-\dfrac{1}{90}\right)\)
\(=2\left(\dfrac{1}{15}-\dfrac{1}{90}\right)=\dfrac{4}{45}\)
bạn có thể giải thích kĩ hơn giúp mình đc ko, chứ nhìn đáp án ntn mk cũng ko hiểu cho lắm
B=\(\dfrac{6}{15.18}+\dfrac{6}{18.21}+...+\dfrac{6}{87.90}\)
B=\(2.\left(\dfrac{3}{15.18}+\dfrac{3}{18.21}+...+\dfrac{3}{87.90}\right)\)
B=\(2.\left(\dfrac{1}{15}-\dfrac{1}{18}+\dfrac{1}{18}-\dfrac{1}{21}+...+\dfrac{1}{87}-\dfrac{1}{90}\right)\)
B=\(2.\left(\dfrac{1}{15}-\dfrac{1}{90}\right)\)
B=\(2.\dfrac{1}{18}\)=\(\dfrac{1}{9}\)
Vậy B<1
Ta có: \(B=\dfrac{6}{15\cdot18}+\dfrac{6}{18\cdot21}+\dfrac{6}{21\cdot24}+...+\dfrac{6}{87\cdot90}\)
\(=2\left(\dfrac{3}{15\cdot18}+\dfrac{3}{18\cdot21}+\dfrac{3}{21\cdot24}+...+\dfrac{3}{87\cdot90}\right)\)
\(=2\left(\dfrac{1}{15}-\dfrac{1}{18}+\dfrac{1}{18}-\dfrac{1}{21}+\dfrac{1}{21}-\dfrac{1}{24}+...+\dfrac{1}{87}-\dfrac{1}{90}\right)\)
\(=2\left(\dfrac{1}{15}-\dfrac{1}{90}\right)\)
\(=2\cdot\dfrac{1}{18}=\dfrac{1}{9}< 1\)
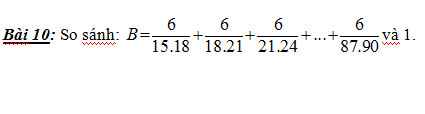
Giải giúp mk với mk đang cần gấp
