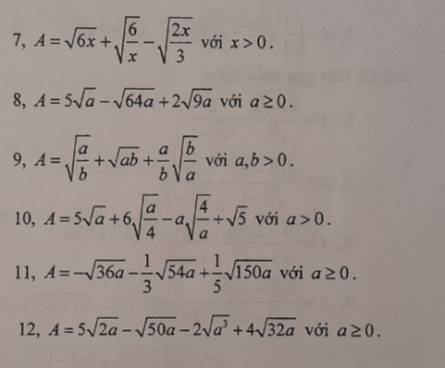7:
\(A=\sqrt{6x}+\sqrt{\dfrac{6}{x}}-\sqrt{\dfrac{2x}{3}}\)
\(=\sqrt{6x}-\sqrt{\dfrac{6x}{9}}+\sqrt{\dfrac{6x}{x^2}}\)
\(=\sqrt{6x}-\dfrac{1}{3}\sqrt{6x}+\dfrac{1}{x}\cdot\sqrt{6x}\)
\(=\sqrt{6x}\left(1-\dfrac{1}{3}+\dfrac{1}{x}\right)=\sqrt{6x}\left(\dfrac{2}{3}+\dfrac{1}{x}\right)\)
8: \(5\sqrt{a}-\sqrt{64a}+2\sqrt{9a}\)
\(=5\sqrt{a}-8\sqrt{a}+2\cdot3\sqrt{a}\)
\(=-3\sqrt{a}+6\sqrt{a}=3\sqrt{a}\)
9: \(\sqrt{\dfrac{a}{b}}+\sqrt{ab}+\dfrac{a}{b}\sqrt{\dfrac{b}{a}}\)
\(=\sqrt{\dfrac{ab}{b^2}}+\sqrt{ab}+\dfrac{a}{\sqrt{a}}\cdot\dfrac{\sqrt{b}}{b}\)
\(=\dfrac{\sqrt{ab}}{b}+\sqrt{ab}+\dfrac{\sqrt{a}}{\sqrt{b}}\)
\(=\dfrac{\sqrt{ab}}{b}+\sqrt{ab}+\dfrac{\sqrt{ab}}{b}\)
\(=\sqrt{ab}\left(\dfrac{2}{b}+1\right)\)
10: \(A=5\sqrt{a}+6\sqrt{\dfrac{a}{4}}-a\sqrt{\dfrac{4}{a}}+\sqrt{5}\)
\(=5\sqrt{a}+6\cdot\dfrac{\sqrt{a}}{2}-a\cdot\dfrac{2}{\sqrt{a}}+\sqrt{5}\)
\(=5\sqrt{a}+3\sqrt{a}-2\sqrt{a}+\sqrt{5}\)
\(=6\sqrt{a}+\sqrt{5}\)
11: \(A=-\sqrt{36a}-\dfrac{1}{3}\cdot\sqrt{54a}+\dfrac{1}{5}\cdot\sqrt{150a}\)
\(=-6\sqrt{a}-\dfrac{1}{3}\cdot3\sqrt{6a}+\dfrac{1}{5}\cdot5\sqrt{6a}\)
\(=-6\sqrt{a}-\sqrt{6a}+\sqrt{6a}\)
\(=-6\sqrt{a}\)
12: \(A=5\sqrt{2a}-\sqrt{50a}-2\sqrt{a^3}+4\sqrt{32a}\)
\(=5\sqrt{2a}-5\sqrt{2a}-2a\sqrt{a}+4\cdot4\sqrt{2a}\)
\(=-2a\sqrt{a}+16\sqrt{2a}\)