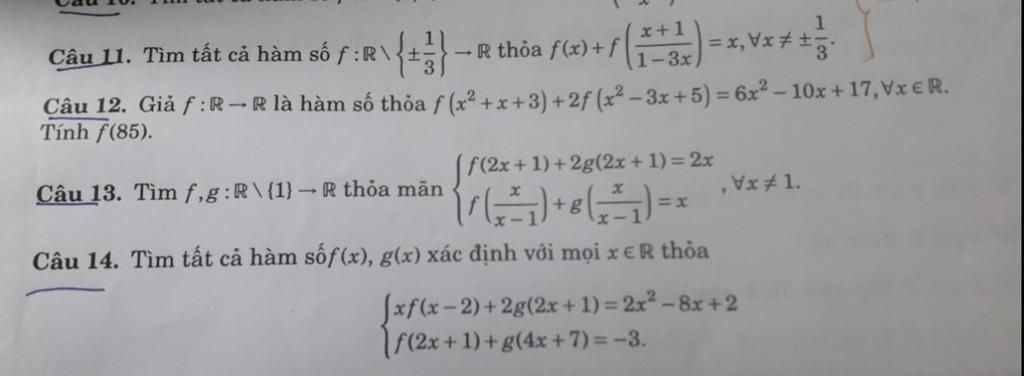Câu 11: Ta có: $f(x)+f\bigg(\dfrac{x+1}{1-3x}\bigg)=x,$ $\forall x\ne\pm\dfrac{1}{3}$ $(1)$
Thế $x\rightarrow\dfrac{x+1}{1-3x}$ vào $(1)$, ta được:
$f\bigg(\dfrac{x+1}{1-3x}\bigg)+f\bigg(\dfrac{x-1}{3x+1}\bigg)=\dfrac{x+1}{1-3x},$ $\forall x\ne\pm\dfrac{1}{3}$ $(2)$
Thế $x\rightarrow\dfrac{x-1}{3x+1}$ vào $(1)$, ta được:
$f\bigg(\dfrac{x-1}{3x+1}\bigg)+f(x)=\dfrac{x-1}{3x+1},$ $\forall x\ne\pm\dfrac{1}{3}$ $(3)$
Cộng $(1)$, $(2)$ và $(3)$ vế theo vế rồi chia cả 2 vế cho `2` ta có:
$f(x)+f\bigg(\dfrac{x+1}{1-3x}\bigg)+f\bigg(\dfrac{x-1}{3x+1}\bigg)=\dfrac{x+\dfrac{x+1}{1-3x}+\dfrac{x-1}{3x+1}}{2},$ $\forall x\ne\pm\dfrac{1}{3}$
$⇒f(x)=\dfrac{9x^3+6x^2-x+2}{18x^2-2},$ $\forall x\ne\pm\dfrac{1}{3}$
Câu 13: Ta có: $f(2x+1)+2g(2x+1)=2x,$ $\forall x\ne1$
Thế $x\rightarrow\dfrac{x-1}{2}$, ta được: $f(x)+2g(x)=x-1,$ $\forall x\ne1$
Mặt khác, $f\bigg(\dfrac{x}{x-1}\bigg)+g\bigg(\dfrac{x}{x-1}\bigg)=x,$ $\forall x\ne1$
Thế $x\rightarrow\dfrac{x}{x-1}$, ta được: $f(x)+g(x)=\dfrac{x}{x-1},$ $\forall x\ne1$
Từ đó, ta dễ dàng suy ra được:
$\begin{cases} f(x)=-x+1-\dfrac{2x}{x-1}\\g(x)=x-1-\dfrac{x}{x-1}\end{cases},$ $\forall x\ne1$