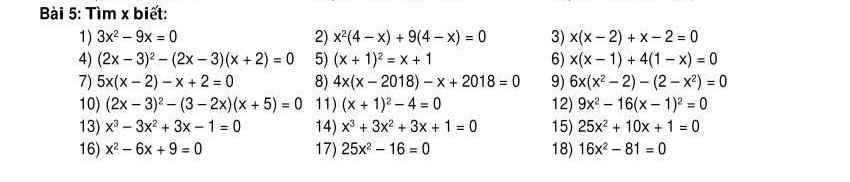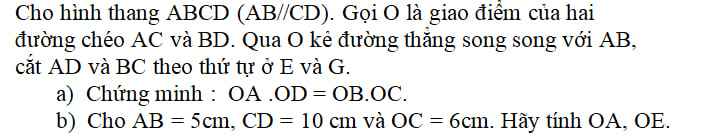giúp tớ với
Bài 8: Cho tam giác \(ABC\) cân tại \(A \left(\hat{A} < 90^\circ \right)\), các đường cao \(BD\) và \(CE\) cắt nhau tại \(H\). Tia phân giác của góc \(ABD\) cắt \(EC\) và \(AC\) theo thứ tự tại \(M\) và \(P\). Tia phân giác của góc \(ACE\) cắt \(DB\) và \(AB\) theo thứ tự tại \(Q\) và \(N\). Chứng minh rằng:
a) \(ABD = ACE\).
b) \(BH = CH\).
c) Tam giác \(BOC\) vuông cân.
d) \(MNPQ\) là hình vuông.
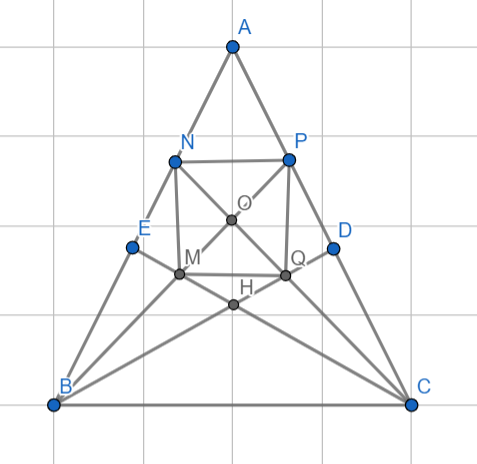
a, Xét `\triangleABD` và `\triangleACE` có:
`\hat{A}` chung
`\hat{ADB}=\hat{AEC}=(90^o)`
`=>\hat{ABD}=\hat{ACE}` `(đpcm)`
b, Ta có: `\hat{ABC}=\hat{ACB}`
`=>\hat{ABC}-\hat{ABD}=\hat{ACB}-\hat{ACE}`
`=> \hat{HBC}=\hat{HCB}`
`=> \triangleBHC` cân tại `H`
`=> HB=HC` `(đpcm)`
c, Ta có: `\hat{ABP}=\hat{PBD}=\hat{ACQ}=\hat{QCE}(=1/2 \hat{ABD}=1/2 \hat{ACE})`
`=> \hat{PBD}+\hat{HBC}=\hat{QCE}+\hat{HCB}`
`=> \hat{OBC}=\hat{OCB}`
`=> \triangleBOC` cân tại `O`
Ta có: `\hat{BOC}=180^o - (\hat{OBC} + \hat{OCB})=180^o - (\hat{OBD} + \hat{OCE} + \hat{HBC} + \hat{HCE})`
`=>\hat{BOC}=180^o - {\hat{ABD} + \hat{HBC} + \hat{HCB})`
`=180^o - (180^o - \hat{BEC})`
`=\hat{BEC}=90^o`
`=> \triangleBOC` vuông cân tại `O` `(đpcm)`
d, Xét `\triangleBMH` và `\triangleCQH` có:
`\hat{MBH}=\hat{QCH}`
`BH=CH`
`\hat{BHM}=\hat{CHQ} (\text{2 góc đối đỉnh})`
`=> \triangleBMH= \triangleCQH(g.c.g)`
`=> BM=CQ`
mà `OB=OC`
`=> OM=OQ`
`\triangleNBQ` có `BO` là đường phân giác và đường cao`=>\triangleNBQ` cân tại `B`
`=>ON=OQ`
`\triangleMCP` có `CO` là đường phân giác và đường cao `=>\triangleMCP` cân tại `C`
`=>OM=OP`
Tứ giác `MNPQ` có 2 đường chéo cắt nhau tại trung điểm mỗi đường `=>MNPQ` là hình bình hành
mà 2 đường chéo `MP=NQ` `=>MNPQ` là hình chữ nhật
mà `MP\botNQ` `=>` tứ giác `MNPQ` là hình vuông `(đpcm)`
