Question

Giúp tớ với ạ, cảm ơn

Answer 1

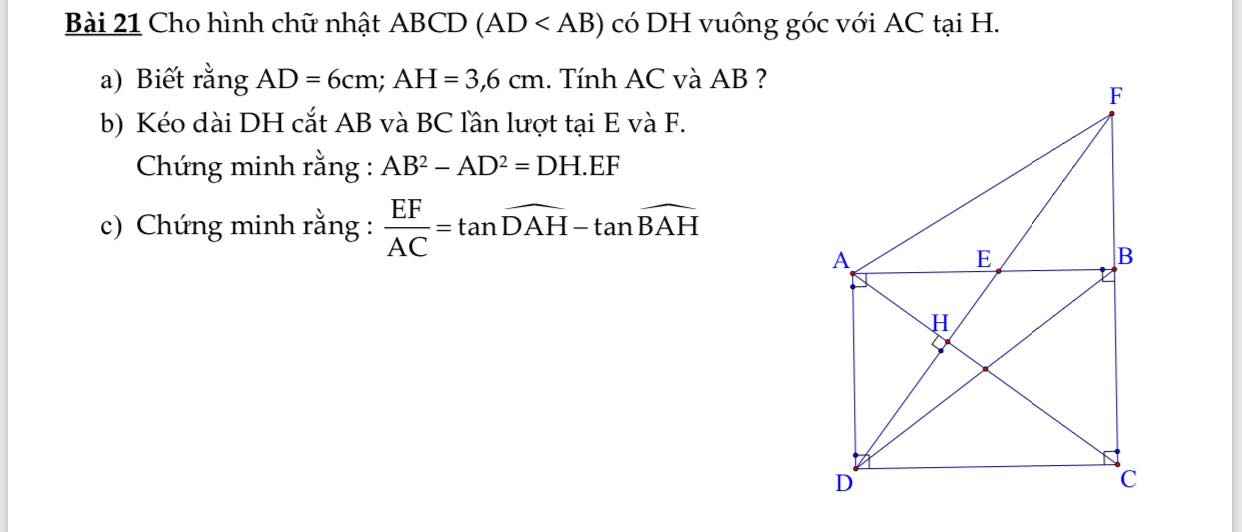
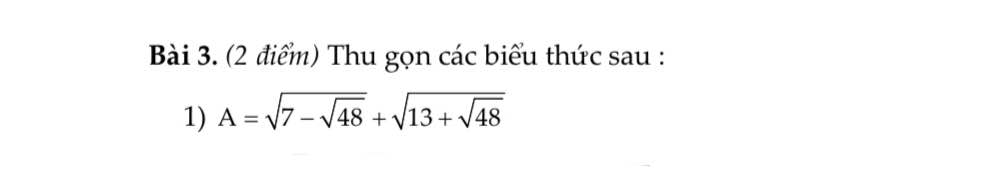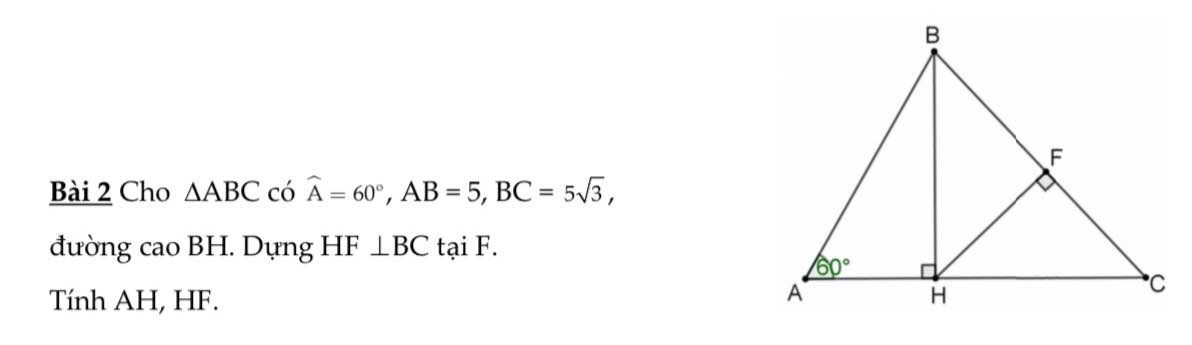\(A=\sqrt{7-\sqrt{48}}+\sqrt{13+\sqrt{48}}\)

\(=\sqrt{7-2.2\sqrt{3}}+\sqrt{13+2.2\sqrt{3}}\)

\(=\sqrt{\left(2-\sqrt{3}\right)^2}+\sqrt{\left(2\sqrt{3}+1\right)^2}\)

\(=2-\sqrt{3}+2\sqrt{3}+1=\sqrt{3}+3\)

Answer 2

Ta có: \(A=\sqrt{7-\sqrt{48}}+\sqrt{13+\sqrt{48}}\)

\(=2-\sqrt{3}+2\sqrt{3}+1\)

\(=3+\sqrt{3}\)