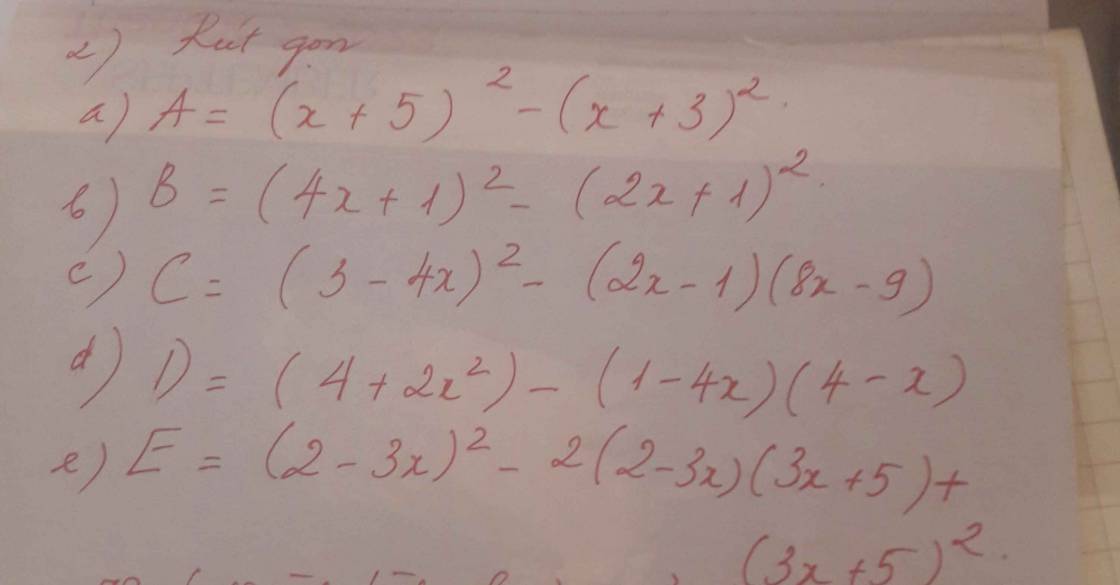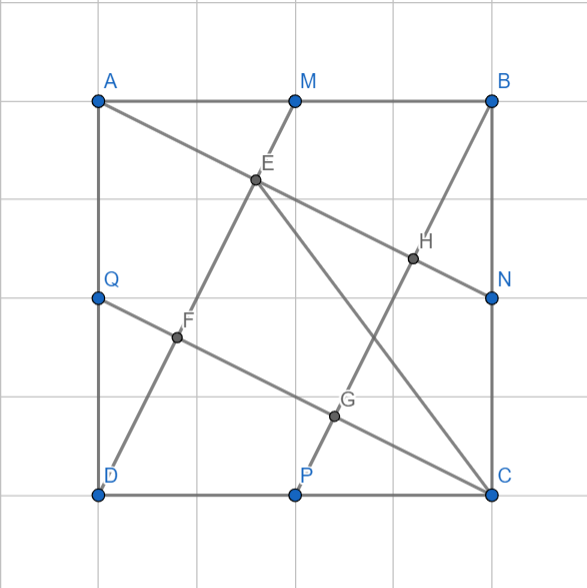
a, Xét `\triangle ANB` và `\triangle DMA` có:
`\hat{ABN}=\hat{DAM}(=90^o)`
`AB=DA`
`NB=MA=(1/2 AB)`
`=> \triangle ANB=\triangle DMA` `(\text{2 cạnh góc vuông})`
`=> {(AN=DM(đpcm)),(\hat{NAB}=\hat{MDA}):}`
Ta có: `\hat{NAB} + \hat{AME}=\hat{AME} + \hat{MDA}`
`=> 180^o - \hat{AEM} = 90^o`
`=> \hat{AEM} = 90^o`
`=> AN \bot DM (đpcm)`
b, Gọi giao điểm của `CQ` và `DM` là `F`, của `CQ` và `BP` là `G`, của `AN` và `BP` là `H`
C/minh tương tự A ta được `{(CQ\botDM),(CQ\botBP),(AN\botBP):}`
Tứ giác `EFGH` có `\hat{HEF}=\hat{EFG}=\hat{FGH}=\hat{GHE}=90^o`
`=>` Tứ giac `EFGH` là hình chữ nhật
`\triangle AEM=\triangle DFQ(ch-gn)`
`=> ME=QF`
`\triangle QFD=\triangle PGC(ch-gn)`
`=> FD=GC`
Ta có: `MD=CQ`
`=> ME+EF+FD=QF+FG+CG`
mà `ME=QF, FD=CG`
`=> EF=FG`
`=>` tứ giác `EFGH` là hình vuông
`=> DM,AN,BP,CQ` giao nhau tạo thành hình vuông `(đpcm)`
c, `\triangle DCF` có `GP//DF,CP=DP`
`=> GP` là đường trung bình của `\triangle DCF`
`=> CG=FG`
`=> EF=DF`
Xét `\triangle ECF` và `\triangle DCF` có:
`\hat{EFC}=\hat{DFC}(=90^o)`
`EF=DF`
`CF` cạnh chung
`=> \triangle ECF=\triangle DCF (\text{2 cạnh góc vuông)`
`=> CE=CD` `(đpcm)`