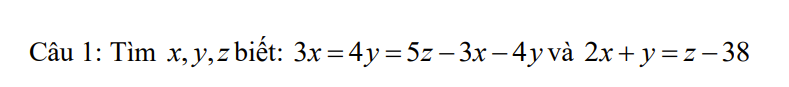Question

giúp tiếp

Answer 1

Answer 2

Ta có: \(2x+y=z-38\Rightarrow2x+y-z=38\)

Vì \(3x=4y=5z-3x-4y\Rightarrow3x=5z-3x-3x\Rightarrow9x=5z\Rightarrow\dfrac{x}{5}=\dfrac{z}{9}\Rightarrow\dfrac{x}{20}=\dfrac{z}{36}\left(1\right)\)

Vì \(3x=4y\Rightarrow\dfrac{x}{4}=\dfrac{y}{3}\Rightarrow\dfrac{x}{20}=\dfrac{y}{15}\left(2\right)\)

Từ (1) và (2) suy ra \(\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{36}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

\(\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{36}=\dfrac{2x+y-z}{40+15-36}=\dfrac{-38}{19}=-2\Rightarrow\left\{{}\begin{matrix}x=-2.20=-40\\y=-2.15=-30\\z=-2.36=-72\end{matrix}\right.\)

Vậy \(x=-40;y=-30;z=-72\)