a) Xét tứ giác BCEF có:
\(\widehat{BFC}=\widehat{BEC}\left(=90^o\right).\)
Mà 2 đỉnh F; E kề nhau, cùng nhìn cạnh BC.
\(\Rightarrow\) Tứ giác BCEF nội tiếp đường tròn (dhnb).
b) Vì tứ giác BCEF nội tiếp đường tròn (cmt).
\(\Rightarrow\widehat{AEF}=\widehat{ABC}.\)
Xét \(\Delta AEF\) và \(\Delta ABC:\)
\(+\widehat{AEF}=\widehat{ABC}\left(cmt\right).\)
\(+\widehat{FAE}\) \(chung.\)
\(\Rightarrow\text{}\text{}\Delta AEF\sim\text{}\text{}\Delta ABC\left(g-g\right).\)
\(\Rightarrow\dfrac{AE}{AB}=\dfrac{EF}{BC}.\\ \Rightarrow AE.BC=EF.AB.\)
Đúng 1
Bình luận (0)
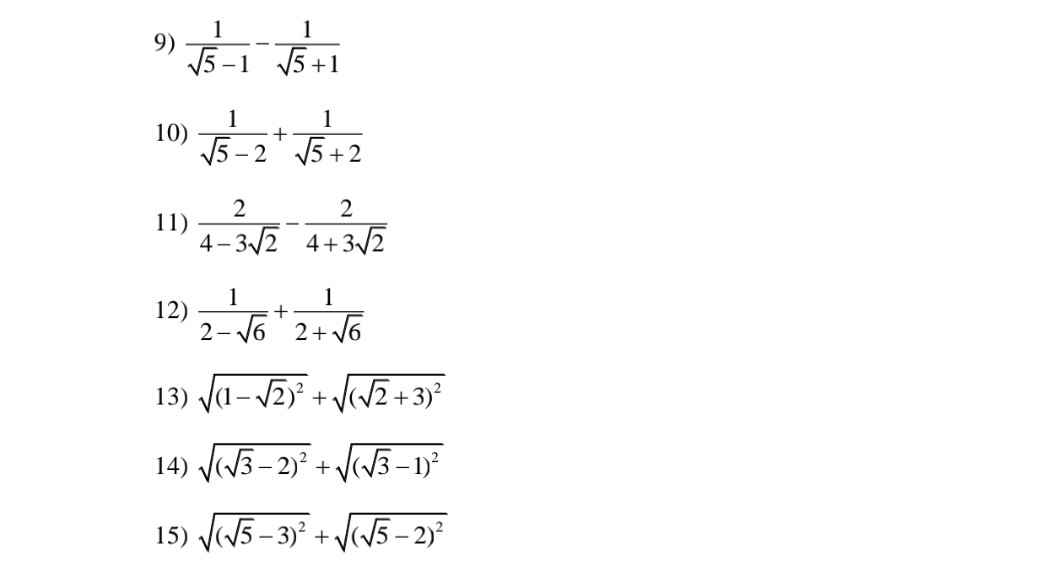
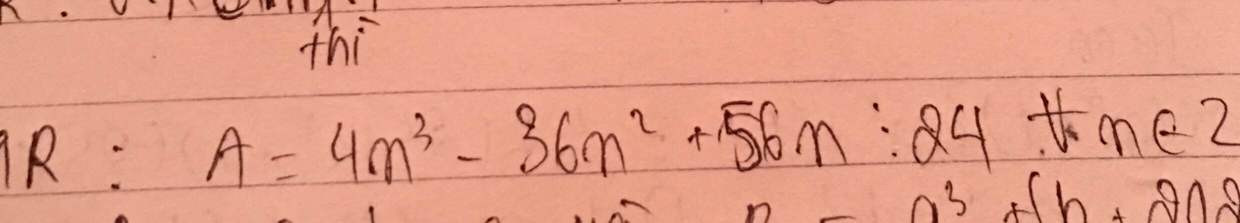
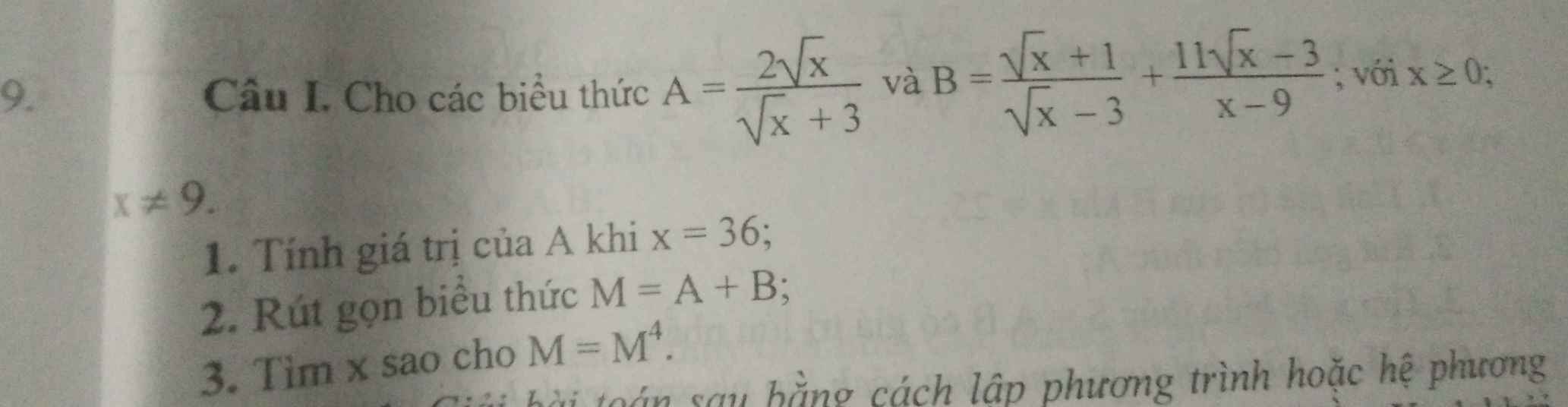
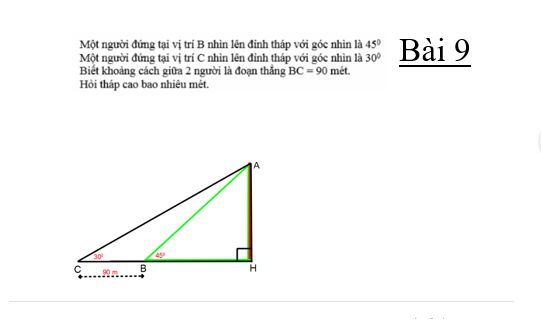giúp em với ạ. Em cảm ơn ạ