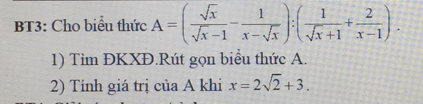1: \(M=\left(\dfrac{x-\sqrt{x}+2}{x-1}-\dfrac{1}{\sqrt{x}-1}\right)\cdot\dfrac{x+2\sqrt{x}+1}{2x-2\sqrt{x}}\)
\(=\left(\dfrac{x-\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}-1}\right)\cdot\dfrac{\left(\sqrt{x}+1\right)^2}{2\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x-\sqrt{x}+2-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\left(\sqrt{x}+1\right)^2}{2\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\cdot\dfrac{\sqrt{x}+1}{2\sqrt{x}}=\dfrac{\sqrt{x}+1}{2\sqrt{x}}\)
2: \(\left\{{}\begin{matrix}x-y=3\\3x-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-3y=9\\3x-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-3y-3x+4y=9-2\\x-y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=7\\x=y+3=7+3=10\end{matrix}\right.\)
3:
a: Khi m=-5/4 thì phương trình sẽ trở thành:
\(x^2-\left(2\cdot\dfrac{-5}{4}+5\right)x+2\cdot\dfrac{-5}{4}+1=0\)
=>\(x^2-\left(-\dfrac{5}{2}+5\right)x-\dfrac{5}{2}+1=0\)
=>\(x^2+\dfrac{5}{2}x-\dfrac{3}{2}=0\)
=>\(2x^2+5x-3=0\)
=>(x+3)(2x-1)=0
=>\(\left[{}\begin{matrix}x=-3\\x=\dfrac{1}{2}\end{matrix}\right.\)
b: \(\text{Δ=(2m+5)^2}-4\cdot\left(2m+1\right)\)
\(=4m^2+20m+25-8m-4\)
\(=4m^2+12m+21=\left(2m+3\right)^2+12>=12>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
Để phương trình (1) có hai nghiệm dương phân biệt thì:
\(\left\{{}\begin{matrix}x_1+x_2>0\\x_1x_2>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2m+5>0\\2m+1>0\end{matrix}\right.\)
=>2m>-1
=>\(m>-\dfrac{1}{2}\)
\(\left|\sqrt{x_1}-\sqrt{x_2}\right|=\sqrt{3}\)
=>\(\left(\sqrt{x_1}-\sqrt{x_2}\right)^2=3\)
=>\(x_1+x_2-2\sqrt{x_1x_2}=3\)
=>\(2m+5-2\sqrt{2m+1}=3\)
=>\(2\sqrt{2m+1}=2m+5-3=2m+2\)
=>\(\sqrt{2m+1}=m+1\)
=>\(\left\{{}\begin{matrix}m>=-1\\2m+1=m^2+2m+1\end{matrix}\right.\)
=>m=0

 GIÚP mình vs;-;
GIÚP mình vs;-;








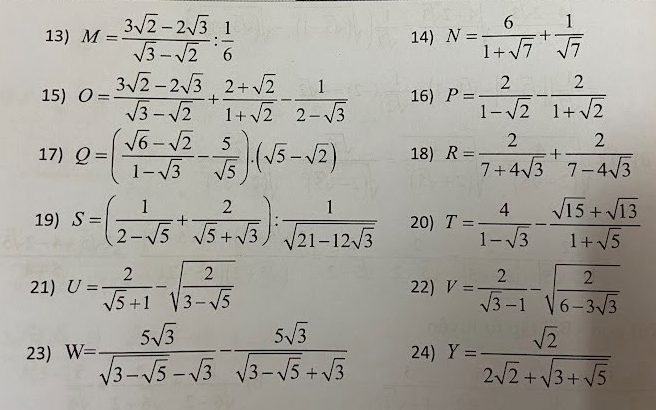

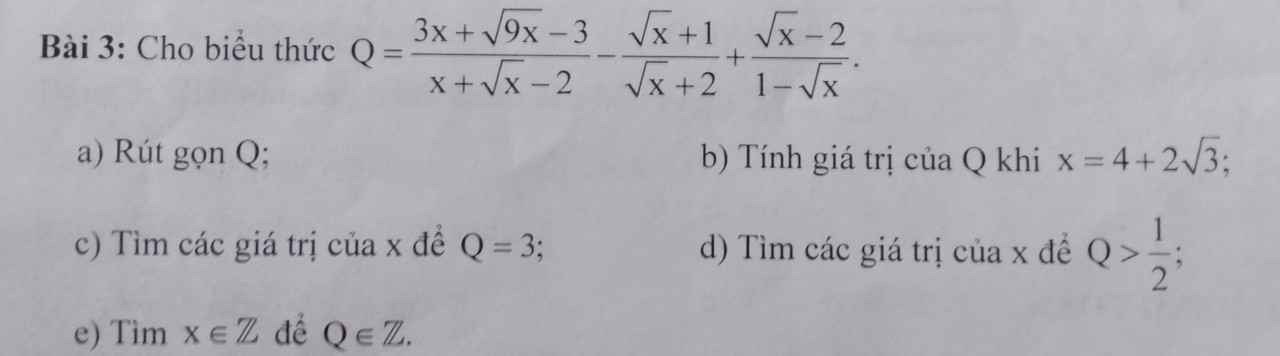 giúp mình vs mình đg cần gấp
giúp mình vs mình đg cần gấp