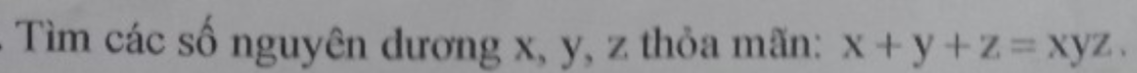Giả sử \(0< x\le y\le z\)
\(\Leftrightarrow xyz=x+y+z\le z+z+z=3z\\ \Leftrightarrow xyz-3z\le0\\ \Leftrightarrow z\left(xy-3\right)\le0\\ \Leftrightarrow xy-3\le0\left(z>0\right)\\ \Leftrightarrow xy\le3\\ \Leftrightarrow xy\le y^2\le3\left(x\le y\right)\)
Mà \(y\in Z\Leftrightarrow y=1\)
\(\Leftrightarrow x+1+z=xz\\ \Leftrightarrow xz-x-z+1=2\\ \Leftrightarrow\left(z-1\right)\left(x-1\right)=2=2\cdot1\left(x,z>0\right)\\ \forall\left\{{}\begin{matrix}z-1=2\\x-1=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\z=3\end{matrix}\right.\\ \forall\left\{{}\begin{matrix}z-1=1\\x-1=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\z=2\end{matrix}\right.\)
Vậy \(\left(x;y;z\right)=\left(1;2;3\right)\) và các hoán vị
giải gấp giúp mình vs, mình cảm ơn
