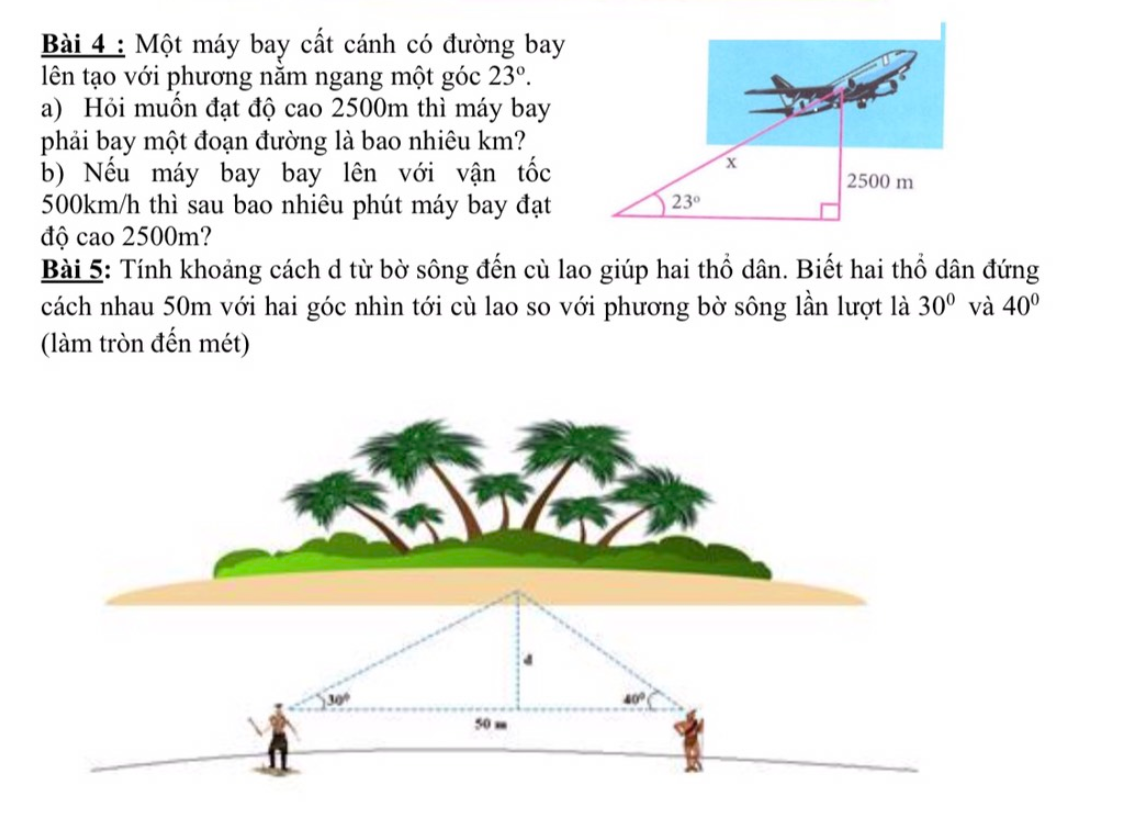
Bài 4:
a) Gọi AB là độ cao máy bay, BC là đoạn đường máy bay bay
Áp dụng tslg trong tam giác ABC vuông tại A:
\(sinC=\dfrac{AB}{BC}\Rightarrow BC=\dfrac{AB}{sinC}=\dfrac{2500}{sin23^0}\approx6398\left(m\right)\)
b) Đổi: \(6398m=6,398km\)
Thời gian máy bay đạt độ cao 2500m:
\(t=\dfrac{S}{v}=\dfrac{6,398}{500}\approx0,03h=1,8ph\)
Bài 5:
Gọi B là góc nhìn \(30^0\) và C là góc nhìn \(40^0\), A là cù lao, kẻ đường cao AH
Áp dụng tslg:
\(\left\{{}\begin{matrix}tanB=\dfrac{AH}{HB}\Rightarrow AH=HB.tan30^0\\tanC=\dfrac{AH}{HC}\Rightarrow AH=HC.tan40^0\end{matrix}\right.\)
\(\Rightarrow\dfrac{HB}{tan40^0}=\dfrac{HC}{tan30^0}=\dfrac{HB+HC}{tan40^0+tan30^0}=\dfrac{BC}{tan40^0+tan30^0}\approx35\left(m\right)\)
\(\Rightarrow HB\approx30\left(m\right)\Rightarrow AH\approx17\left(m\right)\)
Bài 4:
a) Muốn đạt độ cao 2500m thì:
\(sin23^o=\dfrac{2500}{x}\) (hệ thức lượng giác trong tam giác vuông)
\(\Rightarrow x\approx6398,3m\)
b) \(v=500\)km/h=\(\dfrac{1250}{9}\)m/s
Thời gian để máy bay đạt độ cao 2500m:
\(t=\dfrac{S}{v}=\dfrac{2500}{\dfrac{1250}{9}}=18\left(s\right)=0,3\left(phút\right)\)
Bài 5.
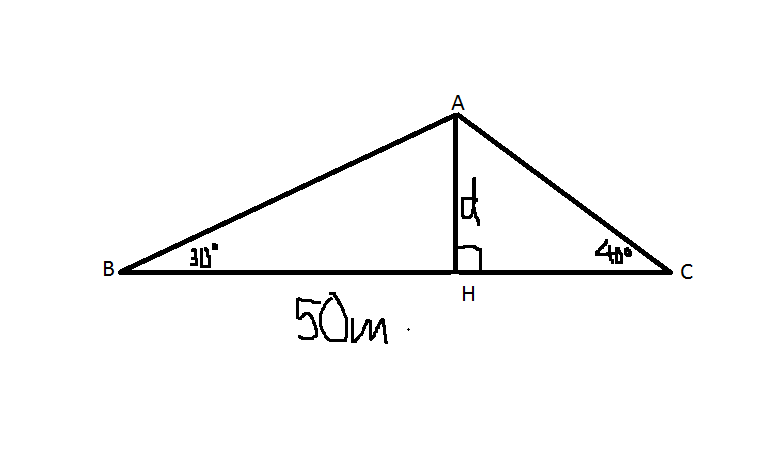
Xét tam giác ABH vuông tại H có:
\(tan30=\dfrac{d}{BH}\Rightarrow BH=\dfrac{d}{tan30}\)
Xét tam giác AHC vuông tại H có:
\(tan40=\dfrac{d}{CH}\Rightarrow CH=\dfrac{d}{tan40}\)
Lại có \(BH+CH=BC\) \(\Rightarrow\) \(\dfrac{d}{tan30}+\dfrac{d}{tan40}=50\Rightarrow d\approx17,1m\)