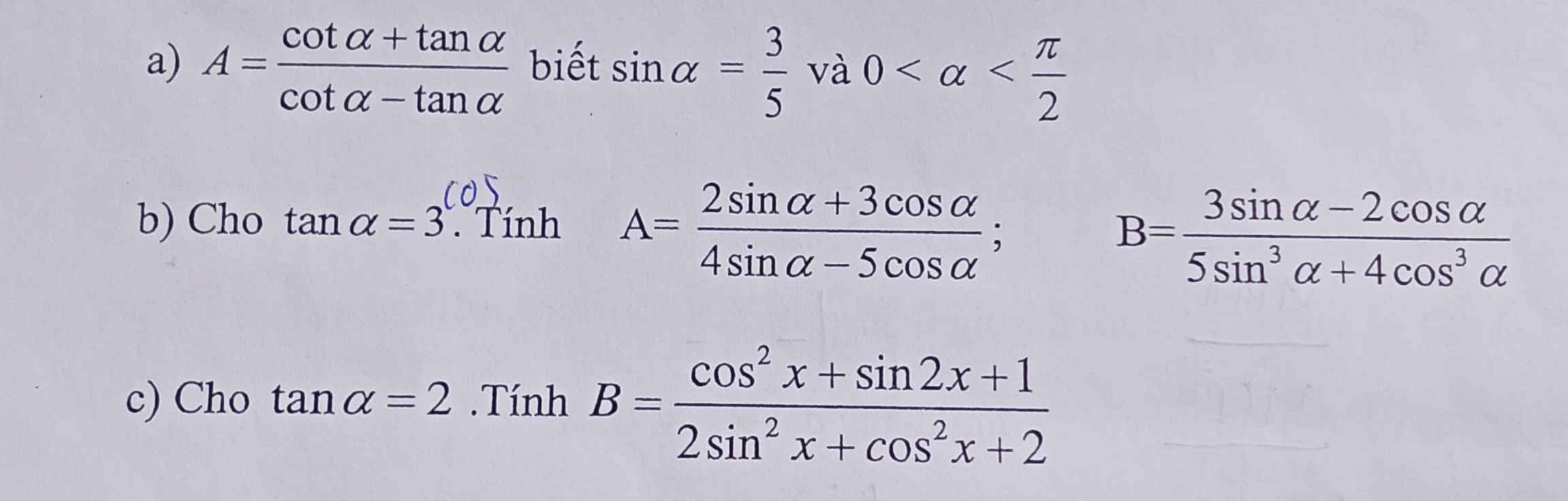a.
\(0< a< \dfrac{\pi}{2}\Rightarrow cosa>0\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{4}{5}\)
\(\Rightarrow tana=\dfrac{sina}{cosa}=\dfrac{3}{4}\) ; \(cota=\dfrac{1}{tana}=\dfrac{4}{3}\)
\(\Rightarrow A=\dfrac{\dfrac{4}{3}+\dfrac{3}{4}}{\dfrac{4}{3}-\dfrac{3}{4}}=...\)
b.
\(A=\dfrac{\dfrac{2sina}{cosa}+\dfrac{3cosa}{cosa}}{\dfrac{4sina}{cosa}-\dfrac{5cosa}{cosa}}=\dfrac{2tana+3}{4tana-5}=\dfrac{2.3+3}{4.3-5}=...\)
\(B=\dfrac{\dfrac{3sina}{cos^3a}-\dfrac{2cosa}{cos^3a}}{\dfrac{5sin^3a}{cos^3a}+\dfrac{4cos^3a}{cos^3a}}=\dfrac{3tana\left(1+tan^2a\right)-2\left(1+tan^2a\right)}{5tan^3a+4}=...\) em tự thay số
c.
\(B=\dfrac{cos^2x+2sinx.cosx+1}{sin^2x+3}=\dfrac{\dfrac{cos^2x}{cos^2x}+\dfrac{2sinx.cosx}{cos^2x}+\dfrac{1}{cos^2x}}{\dfrac{sin^2x}{cos^2x}+\dfrac{3}{cos^2x}}\)
\(=\dfrac{1+2tanx+\left(1+tan^2x\right)}{tan^2x+3\left(1+tan^2x\right)}=...\)