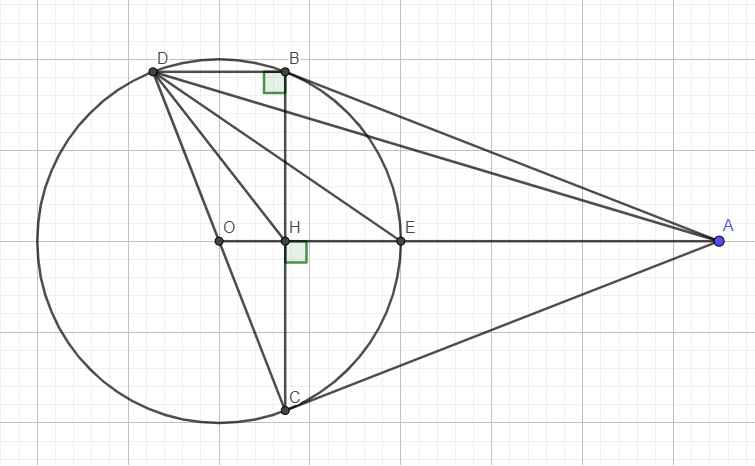
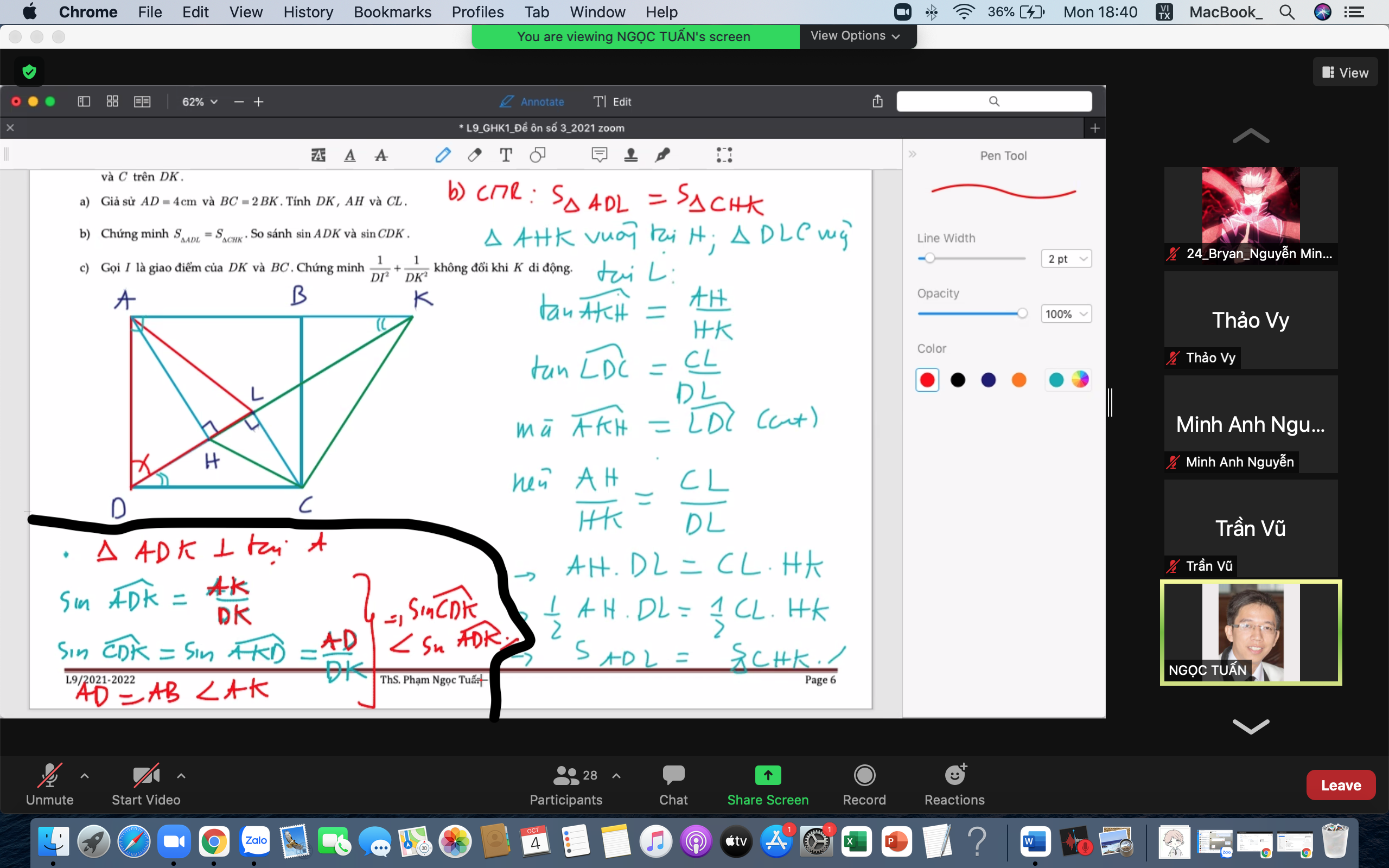
Ta có: \(\widehat{DBC}=90^0\) (nt chắn nửa đường tròn)
\(\Rightarrow BD||OA\) (cùng vuông góc BC)
\(\Rightarrow\widehat{BDE}=\widehat{DEO}\) (slt)
Mà \(\widehat{DEO}=\widehat{ODE}\) (OD=OE=R nên tam giác ODE cân tại O)
\(\Rightarrow\widehat{ODE}=\widehat{BDE}\) (1)
Lại có OH là đường trung bình tam giác BCD (đi qua 2 trung điểm)
\(\Rightarrow BD=2OH\)
Theo câu b: \(BD.OA=2R^2=2OD^2\Rightarrow2OH.OA=2OD^2\)
\(\Rightarrow\dfrac{OH}{OD}=\dfrac{OD}{OA}\)
Hai tam giác ODH và OAD có: \(\left\{{}\begin{matrix}\widehat{O}\text{ chung}\\\dfrac{OH}{OD}=\dfrac{OD}{OA}\end{matrix}\right.\)
\(\Rightarrow\Delta ODH\sim\Delta OAD\Rightarrow\widehat{ODH}=\widehat{OAD}\)
Mà \(\widehat{OAD}=\widehat{BDA}\) (so le trong) (2)
(1);(2) \(\Rightarrow\widehat{HDE}=\widehat{ADE}\) hay DE là phân giác \(\widehat{HDA}\)